7．已知球O的半径为1，A、B、C三点都在球面上，且每两点间的球面距离均为，则球心O到平面ABC的距离为

(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C. 　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

解析：设球心O到平面ABC的距离为h，由等体积法可知，V_O－ABC＝V_C－AOB，即h·S_△ABC＝OC·S_△AOB，即h＝＝＝.

答案：B

6．设M是正四面体ABCD的高线AH上一点，连结MB、MC，若∠BMC＝90°，则的值为

(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．1

解析：设正四面体的棱长为a，MH＝x，则MC²＝MB²＝MH²+BH²＝x²+a²，在Rt△BMC中，由MB²+MC²＝BC²，得2(x²+a²)＝a²，解得x＝a，∴AM＝MH＝AH，即＝1.

答案：D

5．正方体A′B′C′D′－ABCD的棱长为a，EF在AB上滑动，且|EF|＝b(b<a)，Q点在D′C′上滑动，则四面体A′－EFQ的体积为

(　)

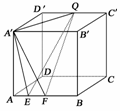
图1

A．与E、F位置有关

B．与Q位置有关

C．与E、F、Q位置都有关

D．与E、F、Q位置均无关，是定值

解析：V_A′－EFQ＝V_Q－A′EF.

答案：D

4．(2010·浙江温州八校联考)已知直线a，如果直线b同时满足条件①a与b异面；②a与b成定角；③a与b的距离为定值，则这样的直线b

(　)

A．唯一确定　 　　　　　　　　　　　　　　　　　　　　　　　 B．有2条

C．有4条　 　　　　　　　　　　　　　　　　　　　　　　　　　 D．有无数条

解析：找出模型，如墙角处考虑D正确．

答案：D

3．(2010·郑州二检)设a、b是两条直线，α、β是两个平面，则a⊥b的一个充分条件是

(　)

A．a⊥α，b∥β，α⊥β　

B．a⊥α，b⊥β，α∥β

C．a⊂α，b⊥β，α∥β　

D．a⊂α，b∥β，α⊥β

解析：依题意易知A，D中的位置关系不确定，故A、D错误；对于B，易知a∥b，故B错误；对于C，因为b⊥β，α∥β，故b⊥α，又a⊂α，所以a⊥b，故C正确．

答案：C

2．平面α⊥平面β的一个充分条件是

(　)

A．存在一条直线l，使得l⊥α，l⊥β

B．存在一个平面γ，使得γ⊥α，γ⊥β

C．存在一个平面γ，使得γ∥α，γ∥β

D．存在一条直线l，使得l⊥α，l∥β

解析：对于A，由l⊥α，l⊥β得α∥β，因此A不正确；对于B，若直线l⊥γ，则任意一个经过直线l的平面都与平面γ垂直，显然可以找到两个都经过直线l但互不垂直的平面α、β，因此B不正确；对于C，由γ∥α，γ∥β只能得出α∥β，因此C不正确；对于D，由l⊥α，l∥β可得α⊥β，因此D正确．

答案：D

1．过空间一点与已知平面垂直的直线有

(　)

A．0条　　　　　　　　　　　　　　　　 B．1条

C．0条或1条　 　　　　　　　　　　　　　　　　　　　　　　 D．无数条

解析：根据线面垂直的定义及其性质定理可知过空间一点与已知平面垂直的直线只有1条，故选B.

答案：B

22．(14分)(2010·内蒙古赤峰统考)如图4，在平面直角坐标系中，N为圆A：(x+1)²+y²＝16上的一点，点

B(1,0)，点M是BN中点，点P在线段AN上，且·＝0.

(1)求动点P的轨迹方程；

(2)试判断以PB为直径的圆与圆x²+y²＝4的位置关系，并说明理由．

解：(1)由点M是BN中点，又·＝0，可知PM垂直平分BN.

所以|PN|＝|PB|，又|PA|+|PN|＝|AN|，

所以|PA|+|PB|＝4，|AB|＝2.

由椭圆定义知，点P的轨迹是以A，B为焦点的椭圆．

设椭圆方程为+＝1(a>b>0)，

由2a＝4,2c＝2，可得a²＝4，b²＝3.

可知动点P的轨迹方程为+＝1.

(2)设点P(x₀，y₀)，PB的中点为Q，则Q(，)，

|PB|＝＝

＝＝2－x₀，

即以PB为直径的圆的圆心为Q(，)，

半径为r₁＝1－x₀，

又圆x²+y²＝4的圆心为O(0,0)，半径r₂＝2，

又|OQ|＝

＝

＝＝1+x₀，

故|OQ|＝r₂－r₁，即两圆内切．

21．(12分)已知圆C的方程为x²+y²＝4.

(1)直线l过点P(1,2)，且与圆C交于A、B两点，若|AB|＝2，求直线l的方程；

(2)圆C上一动点M(x₀，y₀)，＝(0，y₀)，若向量＝+，求动点Q的轨迹方程，并说明轨迹是什么曲线．

解：(1)①若直线l垂直于x轴，则此直线为x＝1，l与圆的两个交点坐标分别为(1，)和(1，－)，这两点间的距离为2，符合题意．

②若直线l不垂直于x轴，设其方程为y－2＝k(x－1)

即kx－y－k+2＝0

设圆心到此直线的距离为d

∵2＝2∴d＝1

∴1＝解得k＝

故所求直线方程为3x－4y+5＝0

综上所述所求直线方程是x＝1或3x－4y+5＝0.

(2)设Q点坐标为(x，y)

∵M点的坐标是(x₀，y₀)，＝(x₀，y₀)，＝(0，y₀)，

＝+

∴(x，y)＝(x_0,2y₀)∴

∵x+y＝4∴x²+()²＝4.即+＝1，

∴Q点的轨迹方程是+＝1.

Q点轨迹是一个焦点在y轴上的椭圆．

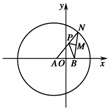
图4

20．(12分)圆C通过不同的三点P(k,0)、Q(2,0)、R(0,1)，已知圆C在P点切线的斜率为1，试求圆C的方程．

解：设圆C的方程为x²+y²+Dx+Ey+F＝0.

将P、Q、R的坐标代入，得

∴圆的方程为x²+y²－(k+2)x－(2k+1)y+2k＝0，圆心为(，)．

又∵k_CP＝－1，∴k＝－3.

∴圆的方程为x²+y²+x+5y－6＝0.