9．设函数f(x)＝sin2x，若f(x+t)是偶函数，则t的一个可能值是__________．

解析：∵f(x+t)＝sin2(x+t)＝sin(2x+2t)是偶函数，

∴f(x+t)＝f(－x+t)，

即sin(2x+2t)＝sin(－2x+2t)．

∴2x+2t＝－2x+2t+2kπ，k∈Z，

或2x+2t＝π－(－2x+2t)+2kπ，k∈Z.

∴t＝π，k∈Z.

答案：，，，…，π(k∈Z)

8．将函数y＝f(x)·sinx(x∈R)的图象向右平移个单位后，再作关于x轴对称变换，得到函数y＝1－2sin²x的图象，则f(x)可以是________．

解析：将y＝f(x)sinx的图象向右平移个单位得

y＝f(x－)sin(x－)的图象，

其关于x轴的对称图象的解析式为

y＝－f(x－)sin(x－)，

∵y＝1－2sin²x＝cos2x＝sin(－2x)

＝2sin(－x)cos(－x)＝－2cos(x－)sin(x－)

∴f(x－)＝2cos(x－)，故f(x)＝2cosx.

答案：2cosx

7．(2009·江苏高考)函数y＝Asin(ωx+φ)(A，ω，φ为常数，A>0，ω>0)在闭区间

　[－π，0]上的图象如图4所示，则ω＝______.

图4

解析：由题图可知，T＝，　 www.k@s@5@　　　　　　　　　　　　　　 高#考#资#源#网

∴ω＝＝3.

答案：3

6．(2009·浙江高考)已知a是实数，则函数f(x)＝1+asinax的图象不可能是

(　)

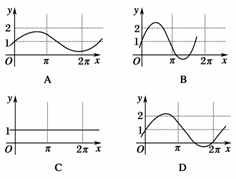
解析：当a＝0时f(x)＝1，C符合，

当0<|a|<1时T>2π，A符合，

当|a|>1时T<2π，B符合．排除A、B、C，故选D.

答案：D

5．方程2sin2x＝x－3的解有

(　)

A．1个　　　　　　 B．2个

C．3个　 　　　　　　　　　　　　　　　　　 D．4个

解析：作y＝sin2x与y＝的图象可得其交点为3个且在x∈(0,2π)上．故选C.

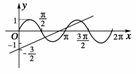
图3

答案：C

4．(2009·辽宁高考)已知函数f(x)＝Acos(ωx+φ)的图像如图2所示，f()＝－，则f(0)等于

(　)

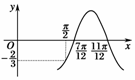
图2

A．－　　　　　　　　　　　　　　　 B．－

C.　 　　　　　　　　　　　　　　　　　　　　 D.

解析：首先由题图可知所求函数的周期为，故ω＝＝3.将(，0)代入解析式，其相当于余弦函数“五点法”作图中的第二关键点，∴+φ＝+2kπ.

∴φ＝－+2kπ.令φ＝－，代入解析式得f(x)＝Acos(3x－)．

又∵f()＝－，f()＝－Acos＝－，

∴f(0)＝Acos(－)＝Acos＝.

答案：C

3．设点P是函数f(x)＝cosωx(其中ω≠0)的图象C的一个对称中心，若点P到图象C的对称轴的距离最小值是π，则函数f(x)的最小正周期是

(　)

A．π　 　　　　　　　　　　　　　　　　　　　 B．2π

C．3π　 　　　　　　　　　　　　　　　　　　 D．4π

解析：由f(x)的图象性质得f(x)的周期为4π，故选D.　 www.k@s@5@　　　　　　　　　　　　　　 高#考#资#源#网

答案：D

2．如图1为函数y＝2sin(ωx+φ)(|φ|

<)的图象，那么

(　)

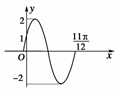
图1

A．ω＝，φ＝

B．ω＝，φ＝－

C．ω＝2，φ＝

D．ω＝2，φ＝－

解析：因图象可由y＝2sinωx左移而得，∴φ>0，又∵图象过(0,1)点，∴φ＝，再由图象过(π，0)，得ω＝2.

故选C.

答案：C

1．将函数y＝sin(6x+)的图象上各点的横坐标伸长到原来的3倍，再向右平移个单位，得到的函数的一个对称中心是

(　)

A．(，0)　　　　　　　 B．(，0)

C．(，0)　 　　　　　　　　　　　　　　　 D．(，0)

解析：将函数y＝sin(6x+)的图象按照条件变换后得到y＝sin2x的图象，故选A.

答案：A

13．(20分)(2009·江苏高考)设向量a＝(4cosα，sinα)，b＝(sinβ，4cosβ)，c＝(cosβ，－4sinβ)．

(1)若a与b－2c垂直，求tan(α+β)的值；

(2)求|b+c|的最大值；

(3)若tanαtanβ＝16，求证：a∥b.

解：(1)因为a与b－2c垂直，

b－2c＝(sinβ－2cosβ，4cosβ+8sinβ)，

所以a·(b－2c)＝4cosαsinβ－8cosαcosβ+4sinαcosβ+8sinαsinβ＝4sin(α+β)－8cos(α+β)＝0，

因此tan(α+β)＝2.

(2)由b+c＝(sinβ+cosβ，4cosβ－4sinβ)，得

|b+c|＝

＝≤4.

又当β＝－时，等号成立，所以|b+c|的最大值为4.

(3)证明：由tanαtanβ＝16得＝，

所以a∥b.