3．(2009·广东高考)一质点受到平面上的三个力F₁、F₂、F₃(单位：牛顿)的作用而处于平衡状态．已知F₁、F₂成60°角，且F₁、F₂的大小分别为2和4，则F₃的大小为

(　)

A．2　 　　　　　　　　　　　　　　　　　 　B．2

C．2　 　　　　　　　　　　　　　　　　　　　 　D．6

解析：如图1设代表力F₁、代表力F₂，则本题实际上是求与的和向量的长度，则余弦定理||²＝||²+||²－2||·||cos∠OF₁G＝4+16－2·2·4·＝28.∴||＝2，故选A.

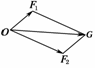
图1

答案：A

2．(2009·山东高考)设P是△ABC所在平面内的一点，+＝2，则

(　)

A.+＝0　 　　　　　　　　B.+＝0

C.+＝0　 　　　　　　　　D.++＝0

解析：∵+＝2，∴－+－＝－2，即+＝0.

答案：B

1．(2009·北京高考)已知向量a、b不共线，c＝ka+b(k∈R)，d＝a－b.如果c∥d，那么

(　)

A．k＝1且c与d同向　　　　 B．k＝1且c与d反向

C．k＝－1且c与d同向 　　　　D．k＝－1且c与d反向

解析：∵c∥d且a，b不共线，

∴存在唯一实数λ使c＝λd.

∴ka+b＝λa－λb，

∴∴故选D.　 www.k@s@5@　　　　　　　　　　　　　　 高#考#资#源#网

答案：D

13．(20分)(2009·石家庄一模)在△ABC中，BC＝2，AC＝，AB＝+1.

(1)求·；

(2)设△ABC的外心为O，若＝m+n，求m，n的值．

解：(1)由余弦定理知：cosA＝＝，

∴·＝||·||cosA＝(+1)·＝+1.

(2)由＝m+n，

知

∴

∵O为△ABC的外心，

∴·＝||·||cos∠BAO

＝||·||·1,2AB,\s\up6(→＝(+1)².

同理，∴·＝1.

即　 www.k@s@5@　　　　　　　　　　　　　　 高#考#资#源#网

解得：

12．(15分)已知a＝(－，)，＝a－b，＝a+b，若△AOB是以O为直角顶点的等腰直角三角形，求向量b及△AOB的面积．

解：∵⊥，∴·＝0，

即(a－b)·(a+b)＝0，∴|a|²－|b|²＝0，

∵|a|＝1，∴|b|＝1.

又||＝|－|＝|2b|＝2，

∴||＝||＝，

即|a+b|＝|a－b|＝，∴a·b＝0.

设b＝(x，y)，则由

解得b＝(，)或(－，－)，

S_△AOB＝||||＝()²＝1.

11．(15分)已知向量a＝e₁－e₂，b＝4e₁+3e₂，其中e₁＝

(1,0)，e₂＝(0,1)．

(1)试计算a·b及|a+b|的值；

(2)求向量a与b夹角的大小．

解：由已知a＝(1，－1)，b＝(4,3)．

(1)a·b＝1×4+(－1)×3＝1，

∵a+b＝(1，－1)+(4,3)＝(5,2)，

∴|a+b|＝＝.

(2)设a，b夹角为θ，

则cosθ＝＝＝，

又θ∈[0，π]，∴θ＝arccos.

10．已知点G是△ABC的重心，＝λ+μ(λ，μ∈R)，那么λ+μ＝________；若∠A＝120°，·＝－2，则||的最小值是__________．

解析：取BC的中点D，则＝＝×(+)＝+，因此λ+μ＝+＝；当∠A＝120°，·＝－2时，||·||cos120°＝－2，||·||＝4，||＝|+|＝≥＝，即||的最小值是.

答案：　

9．如图1，在△ABC中，∠BAC＝120°，AB＝2，AC＝1，D是边BC上一点，DC＝2BD，则·＝________.

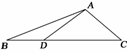
图1

解析：＝+＝+

＝+(－)＝+，

又∵＝－，||²＝1，||²＝4，

∴·＝2×1×cos120°＝－1，

∴·＝(+)·(－)

＝²－²+·＝－，故填－.

答案：－

8．(2009·广东高考)若平面向量a，b满足|a+b|＝1，a+b平行于x轴，b＝(2，－1)，则a＝________.

解析：设a＝(x，y)，则a+b＝(x+2，y－1)，

由题意⇒

∴a＝(－1,1)或(－3,1)．

答案：(－1,1)或(－3,1)

7．(2009·江苏高考)已知向量a和向量b的夹角为30°，|a|＝2，|b|＝，则向量a和向量b的数量积a·b＝________.

解析：a·b＝|a|·|b|·cosθ＝2×cos30°＝2×＝3.

答案：3