13．(20分)已知P点是△ABC内一点，且满足+2+3＝0.设Q为CP的延长线与AB的交点，令＝p，用p表示.

解：∵A、Q、B三点共线，∴＝x+(1－x).

∵+2+3＝0，

∴－+2－2+3＝0.

∴6＝+2.

又∵C、P、Q三点共线，∴＝λ.

∴λ(+)＝x+(1－x).

∴∴λ＝2，∴＝2p.

12．(15分)如图6所示，在△ABC中，D、F分别是BC、AC的中点，＝，＝a，＝b.

图6

(1)用a，b表示向量、、、、；

(2)求证：B、E、F三点共线．

解：(1)延长AD到G，使＝，连结BG、CG，得到▱ABGC，如图7，所以

＝a+b，

＝＝(a+b)，

＝＝(a+b)，

＝＝b，

＝－＝(a+b)－a＝(b－2a)．

　＝－＝b－a＝(b－2a)．

(2)由(1)可知＝，所以B、E、F三点共线．

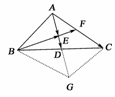
图7

11．(15分)如图5所示，梯形ABCD，AB∥CD，且AB＝2CD，M、N分别为DC和AB的中点，若＝a，＝b，试用a，b表示和.

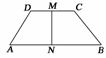
图5

解：解法1：连结CN，N为AB的中点．

∵AN∥DC，且AN＝DC.

∴＝+＝－a+b，

＝－＝+＝－b+a.

解法2：在梯形ABCD中，有+++＝0，

即a++(－)+(－b)＝0，

可得＝b－a.

在四边形ADMN中，有+++＝0，

即有b+a++(－a)＝0，

∴＝a－b.

10．(2009·天津高考)在四边形ABCD中，＝＝(1,1)，\s\up7(|\o(BA,\s\up6(→+\s\up7(|\o(BC,\s\up6(→＝3\s\up7(　，则四边形ABCD的面积为__________．

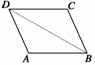
图4

解析：由＝＝(1,1)知AB綊DC.

又\s\up7(|\o(BA,\s\up6(→+\s\up7(|\o(BC,\s\up6(→＝3\s\up7(　知四边形ABCD为菱形，且AB＝AD＝，

又∵\a\vs4\al\co1(\f(1,\o(\s\up7(|\o(BA,\s\up6(→²＝3，

∴∠ABC＝60°，BD＝.

∴∠BAD＝120°，故sin∠BAD＝，

∴S_ABCD＝××＝.

答案：

9．如图3所示，已知一点O到平行四边形ABCD的三个顶点A、B、C的向量为r₁、r₂、r₃，则＝__________.

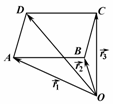
图3

解析：＝+++

＝r₁+(r₂－r₁)+(r₃－r₂)+(r₁－r₂)＝r₃+r₁－r₂.

答案：r₃+r₁－r₂

8．设I为△ABC的内心，当AB＝AC＝5，BC＝6时，＝x+y，则实数x、y的值分别是__________．

解析：如图2，设AI交BC边于D，∵△ABC为等腰三角形，故D为BC中点，BD＝3，在△ABD中，由内角平分线定理可知＝＝.

设＝，又＝+＝+，

∴＝(+)＝+，　 www.k@s@5@　　　　　　　　　　　　　　 高#考#资#源#网

故x＝，y＝.

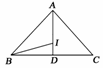
图2

答案：　

7．设a和b是两个不共线的向量，若＝2a+kb，＝a+b，＝2a－b，且A、B、D三点共线，则实数k的值等于__________．

解析：A、B、D三点共线⇔向量与共线，＝2a+kb，＝+＝－a－b+2a－b＝a－2b，由此可解得k＝－4.

答案：－4

6．已知平面内有一点P及△ABC，若++＝，则

(　)

A．点P在△ABC外部　 　　　　　B．点P在线段AB上

C．点P在线段BC上 　　　　　　D．点P在线段AC上

解析：因为++＝⇔+++＝⇔2+＝0，所以P在线段AC上，选择D.

答案：D

5．已知a，b是不共线的向量，若＝λ₁a+b，＝a+λ₂b(λ₁，λ₂∈R)，则A，B，C三点共线的充要条件为

(　)

A．λ₁λ₂－1＝0　 　　　　　　　　B．λ₁＝λ₂＝1

C．λ₁＝λ₂＝－1　 　　　　　　　　D．λ₁λ₂+1＝0

解析：A、B、C三点共线⇔∥⇔λ₁λ₂＝1.故选A.

答案：A

4．已知向量a、b、c中任意两个都不共线，并且a+b与c共线，b+c与a共线，那么a+b+c等于

(　)

A．a　 　　　　　　　　　　　　B．b

C．c　 　　　　　　　　　　　　D．0

解析：由共线向量定理可设a+b＝λ₁c，b+c＝λ₂a，所以b＝λ₁c－a，b＝λ₂a－c.由向量的唯一性可知λ₁＝λ₂＝－1，所以a+b＝－c.

答案：D