8．(2009·河南调研)已知函数f(x)，g(x)分别由下表给出，则f[g(1)]＝__________.

解析：f[g(1)]＝f(3)＝3.

答案：3

7．函数y＝f(x)的图象如图1所示．那么，f(x)的定义域是__________；值域是__________；其中只与x的一个值对应的y值的范围是__________．

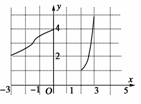
图1

解析：由图象知，函数y＝f(x)的图象包括两部分，一部分是以点(－3,2)和(0,4)为两个端点的一条曲线段，一部分是以(2,1)为起点到(3,5)结束的曲线段，故其定义域是[－3,0]∪[2,3]，值域为[1,5]，只与x的一个值对应的y值的取值范围是[1,2)∪(4,5]．

答案：[－3,0]∪[2,3]　[1,5]　[1,2)∪(4,5]

6．(2010·黄冈质检)平面向量的集合A到A的映射f由f(x)＝x－2(x·a)a确定，其中a为常向量．若映射f满足f(x)·f(y)＝x·y对任意x、y∈A恒成立，则a的坐标可能是　　　　　　　　 　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(　)

A．(，－)　 　　　　　　　　　　　　　　　　　　　 B．(，)　

C．(，)　 　　　　　　　　　　　　　　　　　　　　　　 D．(－，)

解析：由题意得f(x)·f(y)＝[x－2(x·a)a]·[y－2(y·a)a]＝x·y－4(x·a)·(y·a)+4(x·a)·(y·a)·a²＝x·y，即4(x·a)·(y·a)·(a²－1)＝0对于任意x，y∈A恒成立，又x·a与y·a都恒不为零，因此有a²－1＝0，|a|＝1，结合各选项知，选D.

答案：D

5．已知定义在R上的函数f(x)的图象关于点(－，0)对称，且满足f(x)＝－f(x+)，f(－1)＝1，f(0)＝－2，则f(1)+f(2)+f(3)+…+f(2005)的值为　　　　　　　　　　　　　　　　　　 (　)

A．－2　 　　　　　　　　　　　　　　　　　　　　 B．－1

C．0　 　　　　　　　　　　　　　　　　　　　　　　 D．1

解析：∵f(x)的图象关于点(－，0)对称，

∴f(x)＝－f(－x－)．

又f(x)＝－f(x+)，∴f(x)为偶函数．

f(x+3)＝f(x++)＝－f(x+)＝f(x)，

∴f(x)是以3为周期的周期函数．

∴f(1)＝f(－1)＝1，f(0)＝－2＝f(3)，f(2)＝f(－1)＝1.

∴f(1)+f(2)+f(3)＝0.

∴f(1)+f(2)+f(3)+…+f(2005)＝f(2005)＝f(1)＝1.

答案：D

4．(2009·成都诊断性检测)若函数f(x)的定义域为{x|x>}，则函数f()的定义域为(　)

A．{x|x>}　 　　　　　　　　　　　　　　　　 B．{x|x<且x≠0}

C．{x|x>2}∪{x|x<0}　 　　　　　　　　　 D．{x|0<x<2}

解析：由已知得，>⇔2x(x－2)<0⇔0<x<2，选D.

答案：D

3．g(x)＝1－2x，f[g(x)]＝(x≠0)，则f等于　　　　　　　　　　　　　　　　　　　　　 (　)

A．1　　　　　　　　　　 B．3

C．15　 　　　　　　　　　　　　　　　　　　　　　 D．30

解析：令g(x)＝，得x＝，

∴f＝＝15.

答案：C

2．下列各组函数中表示同一函数的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．y＝与y＝

B．y＝lne^x与y＝e^lnx

C．y＝x+3与y＝　

D．y＝x⁰与y＝

解析：选项D中两个函数都表示y＝1(x≠0)这一函数．

选项A中两个函数对应法则不同，分别是：y＝x和y＝|x|.

选项B中两个函数的定义域不同，前者x∈R，而后者x∈(0，+∞)．

选项C中两个函数的定义域不同，前者x∈R，而后者x∈{x|x∈R且x≠1}．

答案：D

1．下列图象中，不可能是函数图象的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

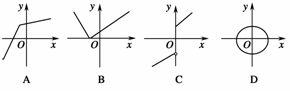
解析：从选项D中图象可以看出x取很多值都对应着两个不同的y值，所以不满足函数的定义．

答案：D

13．(20分)(2010·潮州模拟)已知数列{a_n}、{b_n}分别是等差数列、等比数列，a₃＝8，a₆＝17，b₁＝2，b₁b₂b₃＝9(a₂+a₃+a₄)．

(1)分别求数列{a_n}和{b_n}的通项公式；

(2)设c_n＝log₃b_n，求证：数列{c_n}是等差数列，并求出其公差和首项；

(3)设U_n＝b₁+b₄+b₇+…+b_3n－2，其中n＝1,2，…，求U_n的值．

解：(1)设等差数列{a_n}的首项为a₁、公差为d，等比数列{b_n}的公比为q.

由a₃＝8，a₆＝17得a₁+2d＝8①

a₁+5d＝17②

由①②解得a₁＝2，d＝3，

由b₁b₂b₃＝9(a₂+a₃+a₄)，得8q³＝9×24，解得q＝3.

所以数列{a_n}和{b_n}的通项公式分别为

a_n＝2+(n－1)×3＝3n－1，b_n＝2·3^n－1.

(2)c_n＝log₃b_n＝log₃2·3^n－1＝log₃2+(n－1)，

c_n+1－c_n＝(log₃2+n)－(log₃2+n－1)＝1，

∴数列{c_n}是首项为log₃2，公差为1的等差数列．

(3)由等比数列的性质知数列{b_3n－2}是首项为2，公比为27的等比数列，

所以U_n＝b₁+b₄+b₇+…+b_3n－2

＝＝(27ⁿ－1)．

12．(15分)设数列{a_n}的前n项和为S_n，且(3－m)S_n+2ma_n＝m+3(n∈N^*)．其中m为常数，m≠－3，且m≠0.

(1)求证：{a_n}是等比数列；

(2)若数列{a_n}的公比满足q＝f(m)且b₁＝a₁，

b_n＝f(b_n－1)(n∈N^*，n≥2)，求证：{}为等差数列，并求b_n.

解：(1)由(3－m)S_n+2ma_n＝m+3，

得(3－m)S_n+1+2ma_n+1＝m+3.

两式相减，得(3+m)a_n+1＝2ma_n(m≠－3)．

∴＝(m≠－3)．

从而可以知道，数列{a_n}是等比数列．

(2)当n＝1时，(3－m)a₁+2ma₁＝m+3，a₁＝＝1，

∴b₁＝a₁＝1，又q＝f(m)＝，

∴b_n＝f(b_n－1)＝·(n∈N^*且n≥2)．

得b_nb_n－1+3b_n＝3b_n－1⇒－＝.

∴{}是以1为首项，为公差的等差数列．

∴＝1+＝，故b_n＝.