5．若函数y＝f(x)的值域是[，3]，则函数F(x)＝f(x)+的值域是(　)

A．[，3]　 　　　　　　　　　　　　　　　　　　 B．[2，]

C．[，]　 　　　　　　　　　　　　　　　　　　 D．[3，]

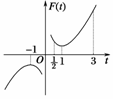
图1

解析：令t＝f(x)，则t∈[，3]，F(t)＝t+，根据其图象可知：

当t＝1时，F(x)_min＝F(t)_min＝F(1)＝2；

当t＝3时，F(x)_max＝F(t)_max＝F(3)＝，

故其值域为[2，]．

答案：B

4．函数y＝x²－2x+3在区间[0，m]上有最大值3，最小值2，则m的取值范围是(　)

A．[1，+∞)　 　　　　　　　　　 　　　　　　　 B．[0,2]

C．(－∞，2]　 　　　　　　　　　　　　　　　　 D．[1,2]

解析：x＝1时，y取最小值2；令y＝3，得x＝0或x＝2.故1≤m≤2.

答案：D

3．函数y＝(x>0)的值域是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．(0，+∞)　 　　　　　　　　　　　　　　　　 B．(0，)

C．(0，]　 　　　　　　　　　　　　　　　　　　 D．[，+∞)

解析：由y＝(x>0)得0<y＝＝≤＝，因此该函数的值域是

(0，]，选C.

答案：C

2．定义在R上的函数y＝f(x)的值域为[a，b]，则y＝f(x+1)的值域为　　　　　 (　)

A．[a，b]　 　　　　　　　　　　　　　　　　　　 B．[a+1，b+1]

C．[a－1，b－1]　 　　　　　　　　　　　　　 D．无法确定

解析：∵函数y＝f(x+1)的图象是由函数y＝f(x)的图象向左平移1个单位得到的，其值域不改变，∴其值域仍为

[a，b]，故应选A.

答案：A

1．若函数y＝2^x的定义域是P＝{1,2,3}，则该函数的值域是　　　　　　　　　　　　　　　 (　)

A．{2,4,6}　　　　　　　 B．{2,4,8}

C．{1,2，log₃2}　 　　　　　　　　D．{1,2，log₂3}

解析：由题意得，当x＝1时，2^x＝2，当x＝2时，2^x＝4，当x＝3时，2^x＝8，即函数的值域为{2,4,8}，故应选B.

答案：B

13．(20分)(2010·宜昌模拟)已知函数f(x)是定义域为R的偶函数，且f(x)＝f(x+2)，当x∈[0,1]时，f(x)＝x.

(1)求x∈[2k－1,2k](k∈Z)时，f(x)的表达式；

(2)若A，B是f(x)图象上纵坐标相等的两点，且A，B两点的横坐标在[0,2]内，点C(1,0)，求△ABC面积的最大值．

解：(1)设x∈[2k－1,2k]，k∈Z，

则2k－x∈[0,1]，那么f(2k－x)＝2k－x.

又f(x)＝f(－x)＝f(－x+2)

＝f(－x+2k)＝2k－x，

∴x∈[2k－1,2k](k∈Z)时，f(x)＝2k－x.

(2)由(1)当x∈[1,2]时，f(x)＝2－x，

函数f(x)的图象关于直线x＝1对称．

设A(1－t,1－t)，B(1+t,1－t)，其中0<t<1，

则AB＝2t，S_△ABC＝·2t·(1－t)≤.

即△ABC面积的最大值是.

12．(15分)设函数f(x)的定义域为R，且满足f(xy)＝f(x)+f(y)．

(1)求f(0)与f(1)的值；

(2)求证：f()＝－f(x)；

(3)若f(2)＝p，f(3)＝q(p，q都是常数)，求f(36)的值．

解：这里的函数f(x)没有给出具体的解析式，(1)中要求f(0)与f(1)的值，就需要对已知条件中的x、y进行恰当的赋值．

(1)令x＝y＝0得f(0)＝f(0)+f(0)，解得f(0)＝0；

令x＝1，y＝0得f(0)＝f(1)+f(0)，解得f(1)＝0.

(2)证明：令y＝，得f(1)＝f()+f(x)，

则f()＝－f(x)．

(3)令x＝y＝2得f(4)＝f(2)+f(2)＝2p，令x＝y＝3得f(9)＝f(3)+f(3)＝2q，令x＝4，y＝9得f(36)＝f(4)+f(9)＝2p+2q.

11．(15分)已知f(x)是一次函数，且满足3f(x+1)－2f(x－1)＝2x+17，求f(x)．

解：求函数解析式的方法有很多种，其中待定系数法是一种常用的方法．

设f(x)＝ax+b(a≠0)，

则3f(x+1)－2f(x－1)＝3ax+3a+3b－2ax+2a－2b＝ax+b+5a＝2x+17，∴a＝2，b＝7，∴f(x)＝2x+7.

10．(2009·湖北八校联考)定义映射f：n→f(n)(n∈N^?)如下表：

若f(n)＝4951，则n＝________.

解析：由f(2)＝f(1)+2，f(3)＝f(2)+3，f(4)＝f(3)+4，归纳可知，f(n)＝f(n－1)+n，累加可知f(n)＝2+2+3+…+n＝+1＝4951，得n(n+1)＝9900，又n∈N^?得n＝99.

答案：99

9．对于实数x、y，定义新运算x*y＝ax+by+1，其中a、b是常数，等式右边是通常的加法和乘法运算，若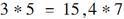　　　

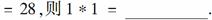
解析：

答案：-11