5．(2009·全国卷Ⅰ)函数f(x)的定义域为R，若f(x+1)与f(x－1)都是奇函数，则(　)

A．f(x)是偶函数 　　　　　　　　　　B．f(x)是奇函数

C．f(x)＝f(x+2)　 　　　　　　　　　　D．f(x+3)是奇函数

解析：由f(x+1)为奇函数，可知f(x)关于点(1,0)对称，

f(x－1)为奇函数，可知f(x)关于点(－1,0)对称，

则f(x)为周期函数且T＝4，

则f(x+3)＝f(x－1)，故选D.

(排除法)若取函数f(x)＝sinπx，g(x)＝cosx，f(x)为奇函数，g(x)为偶函数，

f(x)＝sinπx左、右分别移1个单位都是奇函数，

g(x)＝cosx左、右分别移1个单位也都是奇函数，所以排除A、B.

又f(x)的周期为2，g(x)的周期为4，所以排除C，故选D.

答案：D

4．(2008·福建高考)函数f(x)＝x³+sinx+1(x∈R)，若f(a)＝2，则f(－a)的值为(　)

A．3　 　　　　　　　　　　　　　　　B．0

C．－1 　　　　　　　　　　　　　　D．－2

解析：∵f(a)＝a³+sina+1＝2，

∴a³+sina＝1，

而f(－a)＝－a³－sina+1＝－1+1＝0，故选B.

答案：B

3．已知f(x)＝lg(－ax)是一个奇函数，则实数a的值是　　　　　　　　　　　　　　 (　)

A．1　 　　　　　　　　　　　　　　B．－1

C．10 　　　　　　　　　　　　　　D．±1

解析：据题意知：f(x)+f(－x)＝lg(－ax)+lg(+ax)＝0，

即lg[()²－(ax)²]＝lg[(1－a²)x²+1]＝0，

即(1－a²)x²＝0，而x不恒为0，

则必有1－a²＝0⇒a＝±1，代入检验，函数定义域均关于原点对称．

答案：D

2．设f(x)是增函数，则下列结论一定正确的是　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．y＝[f(x)]²是增函数　　　　　　　 　 B．y＝是减函数

C．y＝－f(x)是减函数　 　　　　　　　　　 　　D．y＝|f(x)|是增函数

解析：根据函数单调性定义判定，设x₁<x₂，

则f(x₁)<f(x₂)，则－f(x₁)>－f(x₂)，

但[f(x₁)]²<[f(x₂)]²，>，

|f(x₁)|<|f(x₂)|，三个关系式不一定成立．

答案：C

1．下列函数中是偶函数的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

①f(x)＝lg(1+x²)　 　　　　　　　②g(x)＝2－|x|

③h(x)＝tan2x　 　　　　　　　　　④s(x)＝

A．①②　 　　　　　　　　　 　　　　　　　　　　　　　　 B．①④

C．②④　 　　　　　　　　　　　　　　　　　　　　　　　 D．①②④

解析：f(x)，g(x)，h(x)显然为偶、偶、奇函数．

对于s(x)，

当x<－1时，s(x)＝x+2，s(－x)＝x+2＝s(x)．

当x>1时，s(x)＝－x+2，s(－x)＝－x+2＝s(x)；

|x|≤1时，s(x)＝0，s(－x)＝0＝s(x)．　

∴s(x)也为偶函数．

答案：D

10．(2009·泉州质检)在实数的运算法则中，我们补充定义一种新运算“?”如下：当a≥b时，a?b＝a；当a<b时，a?b＝b²；则函数f(x)＝(1?x)·x－(2?x)，(x∈[－2,2])的最大值是__________．

解析：

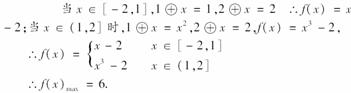
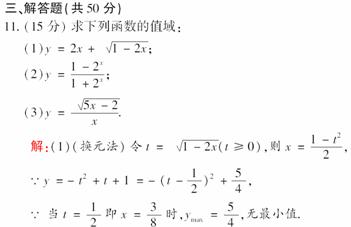
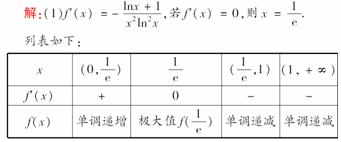
9．函数f(x)＝+2的最小值为__________．

解析：由⇒

∴x≥4或x≤0.

又x∈[4，+∞)时，f(x)单调递增⇒f(x)≥f(4)＝1+2；而x∈(－∞，0]时，f(x)单调递减⇒f(x)≥f(0)＝0+4＝4.

故最小值为1+2.

答案：1+2

8．已知f(x)的值域是[，]，g(x)＝f(x)+，则y＝g(x)的值域是__________．

解析：∵f(x)∈[，]，则2f(x)∈[，]，

1－2f(x)∈[，]．

令t＝∈[，]，

则f(x)＝，g(x)＝+t，

即g(x)＝，对称轴t＝1，

g(x)在t∈[，]上单调递增，g(x)∈[，]．

答案：[，]

7．函数y＝的值域是{y|y≤0或y≥4}，则此函数的定义域为__________．

解析：y＝＝2+，

即≤－2或≥2，

由≤－2⇒≤x<3，

由≥2⇒3<x≤.

答案：[，3)∪(3，]

6．(2009·海南/宁夏高考)用min{a，b，c}表示a，b，c三个数中的最小值．设f(x)＝min{2^x，x+2,10－x}(x≥0)，则f(x)的最大值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．4　 　　　　　　　　　　　　　　　　　　　 B．5

C．6　 　　　　　　　　　　　　　　　　　　　 D．7

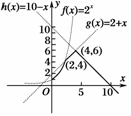
图2

解析：令2^x＝x+2⇒x₁<0(舍)或x₂＝2，

令2^x＝10－x即2^x+x＝10，则2<x<3.

则可知f(x)的大致图象如图2所示．

故f(x)≤6，即选C.

答案：C