2．函数f(x)＝2^x+1的反函数的图象大致是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

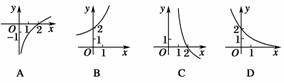
解析：由y＝2^x+1得x+1＝log₂y，x＝log₂y－1(y>0)，即函数f(x)＝2^x+1的反函数是f^－1(x)＝log₂x－1(x>0)，注意到函数f^－1(x)在(0，+∞)上是增函数，结合各选项知，选A.

答案：A

1．设函数f(x)＝log₂x+3，x∈[1，+∞)，则f^－1(x)的定义域是　　　　　　　　　　　　　 (　)

A．(0,1)　 　　　　　　　　　　　　　　　　 B．[1，+∞)

C．[3，+∞)　 　　　　　　　　　　　　 D．R

解析：由x≥1，得log₂x≥0，

∴y＝log₂x+3≥3，

∵反函数的定义域就是原函数的值域，

∴f^－1(x)的定义域为[3，+∞)．

答案：C

13．(20分)(2009·湖北模拟)已知函数f(x)＝x|x+m|+n，其中m，n∈R.

(Ⅰ)求证：m²+n²＝0是f(x)是奇函数的充要条件；

(Ⅱ)若常数n＝－4，且f(x)<0对任意x∈[0,1]恒成立，求m的取值范围．

证明：(Ⅰ)充分性：若m²+n²＝0，则m＝n＝0，

∴f(x)＝x|x|，

又有f(－x)＝－x|－x|＝－x|x|＝－f(x)，∴f(x)为奇函数．

必要性：若f(x)为奇函数，∵x∈R，∴f(0)＝0，即n＝0，∴f(x)＝x|x+m|.

由f(1)＝－f(－1)，有|m+1|＝|m－1|，∴m＝0.

∴f(x)为奇函数，则m＝n＝0，即m²+n²＝0.

∴m²+n²＝0是f(x)为奇函数的充要条件．

解：(Ⅱ)若x＝0时，m∈R，f(x)<0恒成立；

若x∈(0,1]时，原不等式可变形为|x+m|<－.

即－x+<m<－x－.

∴只需对x∈(0,1]，满足　

对①式f₁(x)＝－x+在(0,1]上单调递减，

∴m<f₁(1)＝3.　　　　　　　　　　　　　 ③

对②式，设f₂(x)＝－x－，根据单调函数的定义可证明f₂(x)在(0,1]上单调递增，

∴f₂(x)_max＝f(1)，∴m>f₂(1)＝－5 　　　　　④

由③④知－5<m<3.

12．(15分)设f(x)是周期函数，且最小正周期为2，且f(1+x)＝f(1－x)，当－1≤x≤0时，f(x)＝－x，试求函数f(x)在区间[－1,3]上的表达式．

解：∵f(－x)＝f(2－x)＝f[1+(1－x)]

＝f[1－(1－x)]＝f(x)，∴f(x)是偶函数．

于是由“当－1≤x≤0时，f(x)＝－x”可知当0≤x≤1时，f(x)＝x；

进而当1≤x≤2时，－1≤x－2≤0⇒f(x)＝f(x－2)＝－(x－2)＝－x+2；

当2≤x≤3时，0≤x－2≤1⇒f(x)＝f(x－2)＝x－2.

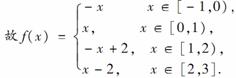
11．(15分)已知函数y＝f(x)(x∈R且x≠0)，对任意非零实数x₁，x₂恒有f(x₁·x₂)＝f(x₁)+f(x₂)，试判断函数f(x)的奇偶性．

解：令x₁＝－1，x₂＝x得：

f(－x)＝f(－1)+f(x)　　　　　　　　　　　　 ①

再令x₁＝1，x₂＝－1得：

f(－1)＝f(1)+f(－1)，即f(1)＝0　　　　　　　 ②

再取x₁＝x₂＝－1得：

f(1)＝f(－1)+f(－1)　　　　　　　　　　　　 ③

由②、③得：f(－1)＝0，

代入①得：f(－x)＝f(x)

∴f(x)为偶函数．

10．已知函数y＝f(x)是R上的偶函数，对于x∈R都有f(x+6)＝f(x)+f(3)成立，且f(－4)＝－2，当x₁，x₂∈[0,3]，且x₁≠x₂时，都有>0.则给出下列命题：

①f(2008)＝－2；

②函数y＝f(x)图像的一条对称轴为x＝－6；

③函数y＝f(x)在[－9，－6]上为减函数；

④方程f(x)＝0在[－9,9]上有4个根．

其中所有正确命题的序号为________．

解析：当x＝－3时，f(－3+6)＝f(－3)+f(3)＝2f(3)，∴f(3)＝0，∴f(x+6)＝f(x)，即函数y＝f(x)是周期为6的偶函数，∴x＝－6为其一条对称轴；又f(－4)＝－2，∴f(2008)＝f(334×6+4)＝f(4)＝f(－4)＝－2；由题意函数y＝f(x)在区间[0,3]上单调递增，又函数y＝f(x)是周期为6的偶函数，∴y＝f(x)在[－9，－6]上单调递减；∵f(3)＝f(9)＝f(－3)＝f(－9)＝0，∴f(x)＝0在区间[－9,9]上有4个根，综上应填①②③④.

答案：①②③④

9．设周期为4的奇函数f(x)的定义域为R，且当x∈[4,6)时，f(x)＝2－x²，则f(－1)的值为__________．

解析：∵f(－1)＝－f(1)＝－f(1+4)＝－f(5)＝－(2－5²)＝23.

答案：23

8．(2008·上海高考)设函数f(x)是定义在R上的奇函数．若当x∈(0，+∞)时，f(x)＝lgx，则满足f(x)>0的x的取值范围是__________．

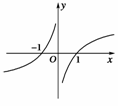
图1

解析：根据题意画出函数f(x)的草图，由图象可知f(x)>0的x的取值范围是－1<x<0或x>1.

答案：(－1,0)∪(1，+∞)

7．(2009·重庆高考)若f(x)＝+a是奇函数，则a＝________.

解析：∵f(x)是{x|x≠0}上的奇函数，

∴f(－1)＝－f(1)．∴a＝.

答案：

6．(2009·四川高考)已知函数f(x)是定义在实数集R上的不恒为零的偶函数，且对任意实数x都有xf(x+1)＝(1+x)f(x)，则f(f())的值是　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．0　 　　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C．1　 　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

解析：由已知令x＝0，则f(0)＝0，

由已知令x＝－，得－f()＝f(－)＝f()，∴f()＝0.

又令x＝，得f()＝f()，

又∵f()＝0，∴f()＝0.

再令x＝，得f()＝f()，

∵f()＝0，∴f()＝0.

∴f(f())＝f(0)＝0.

答案：A