
题目列表(包括答案和解析)
8. 试判断方程sinx=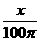 实数解的个数.
实数解的个数.
7. 已知二次函数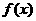 对任意
对任意 ,都有
,都有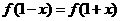 成立,设向量
成立,设向量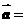 (sinx,2),
(sinx,2),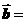 (2sinx,
(2sinx,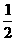 ),
),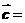 (cos2x,1),
(cos2x,1),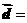 (1,2),当
(1,2),当 [0,
[0,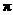 ]时,求不等式f(
]时,求不等式f(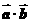 )>f(
)>f(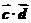 )的解集.
)的解集.
6. 若函数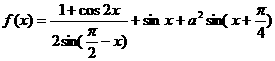 的最大值为
的最大值为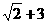 ,试确定常数a的值.
,试确定常数a的值.
5. 设函数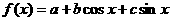 的图象经过两点(0,1),(
的图象经过两点(0,1),(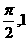 ),且在
),且在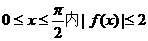 ,求实数a的的取值范围.
,求实数a的的取值范围.
4. 已知向量 = (
= ( ,2),
,2),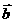 =(
=(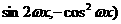 ,(
,(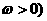 。
。
(1)若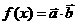 ,且
,且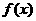 的最小正周期为
的最小正周期为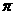 ,求
,求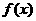 的最大值,并求
的最大值,并求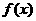 取得最大值时
取得最大值时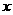 的集合;
的集合;
(2)在(1)的条件下,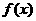 沿向量
沿向量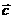 平移可得到函数
平移可得到函数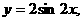 求向量
求向量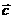 。
。
3. 已知函数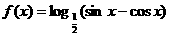 ,
,
(1)求它的定义域和值域;(2)求它的单调区间;(3)判断它的奇偶性;
(4)判断它的周期性,如果是周期函数,求出它的最小正周期。
1.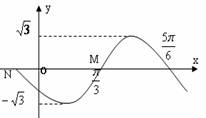 右图为
右图为 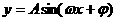 的图象的一段,求其解析式。
的图象的一段,求其解析式。
2 设函数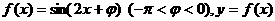 图像的一条对称轴是直线
图像的一条对称轴是直线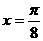 。
。
(Ⅰ)求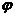 ;(Ⅱ)求函数
;(Ⅱ)求函数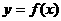 的单调增区间;
的单调增区间;
(Ⅲ)画出函数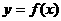 在区间
在区间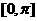 上的图像。
上的图像。
13.(20分)已知函数f(x)=lnx-.
(Ⅰ)判定函数f(x)的单调性;
(Ⅱ)设a>1,证明:<.
解:(Ⅰ)∵f′(x)=-
=-=-
==-.
又∵函数f(x)的定义域为x>0,
∴≤0,
而在(0,+∞)上,只有当x=1时,f′(x)=0,
∴f(x)是定义域上的减函数.
(Ⅱ)由(Ⅰ)f(x)是定义域上的减函数,
∴当a>1时,f(a)<f(1),
即lna-<0,即lna<,
又∵a-1>0,∴<成立.
12.(15分)函数f(x)的定义域为D={x|x>0},且满足:对于任意m,n∈D,都有f(m·n)=f(m)+f(n).
(1)求f(1)的值;
(2)如果f(2)=1,f(3x+1)+f(2x-6)≤2,且f(x)在
(0,+∞)上是单调增函数,求x的取值范围.
解:(1)令m=n=1,有f(1×1)=f(1)+f(1),解得f(1)=0.
(2)f(4)=f(2×2)=f(2)+f(2)=2,所以f(3x+1)+f(2x-6)≤2⇔f(3x+1)+f(2x-6)≤f(4).
因为f(x)在(0,+∞)上是单调增函数,所以f(3x+1)+f(2x-6)≤f(4)⇔
⇔3<x≤,故x的取值范围为(3,].
11.(15分)已知函数f(x)=(x∈R),求f(x)的单调区间,并加以证明.
解:解法1:由函数的单调区间(增区间,减区间)的定义入手分析,取x1<x2,分析f(x1)-f(x2)的符号,由此找出单调增区间与单调减区间.
∵f(x)=(x∈R)是奇函数,
∴只需研究(0,+∞)上f(x)的单调区间即可.
任取x1,x2∈(0,+∞),且x1<x2,则
f(x1)-f(x2)=-=.
∵x+1>0,x+1>0,x2-x1>0,
而x1,x2∈(0,1)时,x1x2-1<0;
x1,x2∈[1,+∞)时,x1x2-1≥0,
∴当x1,x2∈(0,1)时,f(x1)-f(x2)<0,函数f(x)是增函数;
当x1,x2∈[1,+∞)时,f(x1)-f(x2)≥0,函数f(x)是减函数.
又f(x)是奇函数,∴f(x)在(-1,0)上是增函数,在
(-∞,-1]上是减函数.
又x∈[0,1),u∈(-1,0]上恒有f(x)≥f(u),等号只在x=u=0时取到,故f(x)在(-1,1)上是增函数.
综上知,函数f(x)在(-1,1)上是增函数,在(-∞,-1]和[1,+∞)上是减函数.
解法2:f′(x)=()′=,
f′(x)>0⇒x∈(-1,1),即在(-1,1)上函数单调递增.
f′(x)≤0⇒x∈[1,+∞)∪(-∞,-1]即在(-∞,-1]和[1,+∞)上函数单调递减.
综上知,函数f(x)的单调增区间为(-1,1),单调减区间为(-∞,-1]和[1,+∞).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com