
题目列表(包括答案和解析)
4、( )等比数列{an}中,已知对任意自然数n,a1+a2+a3+…+an=2n-1,则
a12+a22+a32+…+an2等于(A)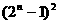 (B)
(B)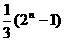 (C)
(C)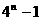 (D)
(D) 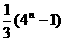
( )5已知数列{an}的前n项和为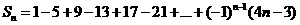 则
则
 的值为 A 13 B-76 C46 D 76
的值为 A 13 B-76 C46 D 76
3、( )数列{an}前n项的和Sn=3n+b(b是常数),若这个数列是等比数列,那么b为
(A)3 (B) 0 (C)-1 (D)1
2、( )数列1,x,x2,…,xn-1,…的前n项之和是
(A)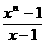 (B)
(B)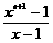 (C)
(C)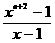 (D)以上均不正确
(D)以上均不正确
1、( )等差数列{an}的前n项和为Sn,若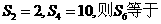
A.12 B.18 C.24 D.42
1、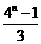 2、
2、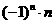 3、
3、 4、
4、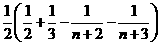 5、
5、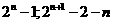 6
6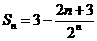 、
、
例1已知数列{an}是等差数列,且a1=2,a1+a2+a3=12.
(1)求数列{an}的通项公式; (2)令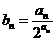 ,求数列{bn}前n项和
,求数列{bn}前n项和
解:(1)由已知得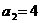 ,又a1=2,
,又a1=2,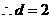 ,
,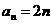
(2)由(1)知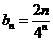 ,又错位相减得数列{bn}前n项和
,又错位相减得数列{bn}前n项和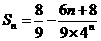
例2、已知二次函数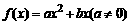 ,其导函数为
,其导函数为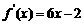 ,数列
,数列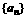 的前
的前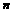 项和为
项和为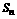 ,点
,点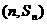 (nÎN*) 均在函数
(nÎN*) 均在函数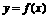 的图像上.(Ⅰ)求数列
的图像上.(Ⅰ)求数列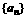 的通项公式;
的通项公式;
(Ⅱ)设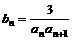 ,
,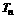 是数列
是数列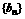 的前
的前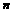 项和,求使得
项和,求使得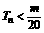 对所有nÎN*都成立的最小正整数
对所有nÎN*都成立的最小正整数 ;
;
解:(Ⅰ)依题设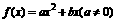 ,由
,由 又由
又由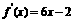 得
得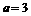 ,
,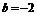 ,∴
,∴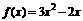 ,所以
,所以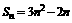 ,
,
当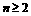 时
时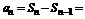
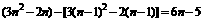 ,
,
当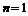 时,
时,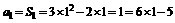 也符合,∴
也符合,∴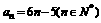 .
.
(Ⅱ)由(Ⅰ)得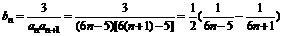 ,
,
∴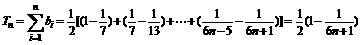 ,
,
∴要使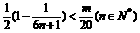 恒成立,只要
恒成立,只要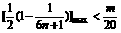 ,
,
又∵ ,∴只要
,∴只要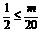 ,即
,即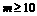 ,∴
,∴ 的最小整数为10
的最小整数为10
例3已知数列{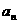 }中的相邻两项
}中的相邻两项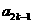 、
、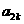 是关于x的方程
是关于x的方程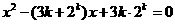 的两个根,且
的两个根,且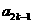 ≤
≤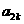 (k =1,2,3,…). (I)求
(k =1,2,3,…). (I)求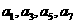 及
及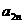 (n≥4); (Ⅱ)求数列{
(n≥4); (Ⅱ)求数列{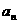 }的前2n项和S2n.
}的前2n项和S2n.
方程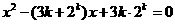 的两个根为
的两个根为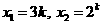 .
.
当k=1时,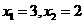 ,所以
,所以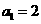 ;当k=2时,
;当k=2时,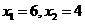 ,所以
,所以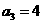 ;
;
当k=3时, ,所以
,所以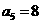 ;当k=4时,
;当k=4时,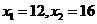 ,所以
,所以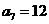 ;
;
因为n≥4时,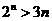 ,所以
,所以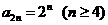
(Ⅱ)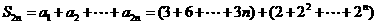 =
=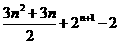
同步练习
5. 数列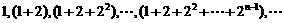 的通项公式
的通项公式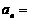 ,前n项和
,前n项和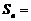
6 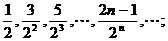 的前n项和为_________
的前n项和为_________
3.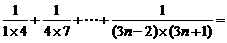 .4.
.4. 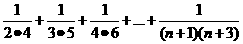 =__________
=__________
2.设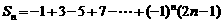 ,则
,则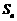 =_______________________.
=_______________________.
5、裂项相消法:把一个数列的各项拆成两项之差,即数列的每一项均可按此法拆成两项之差,在求和时一些正负项相互抵消,于是前n项之和变成首尾若干少数项之和,这一求和方法称为裂项相消法。常见的拆项公式:(1) = ( -)(其中{an}是一个公差为d的等差数列;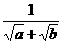 = ( - ); n·n!=(n+1)! - n!;
= ( - ); n·n!=(n+1)! - n!;
⑵
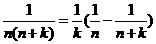 ; ⑶
; ⑶ 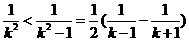
⑷ 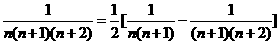 ⑸
⑸
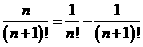
⑹ 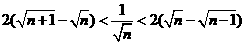 ⑺
⑺
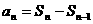
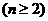
基本练习1.等比数列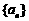 的前n项和Sn=2n-1,则
的前n项和Sn=2n-1,则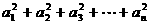 =________________.
=________________.
4、错项相减法:如果一个数列的各项是由一个等差数列与一个等比数列的对应项相乘所组成,此时求和可采用错位相减法。特征:所给数列{a },其中a
},其中a =cn·bn{cn}是一个等差数列,{bn}是一个等比数列。(“等比数列”的求和)
=cn·bn{cn}是一个等差数列,{bn}是一个等比数列。(“等比数列”的求和)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com