
题目列表(包括答案和解析)
3.如果函数y=f(x)的图象如图1,那么导函数y=f′(x)的图象可能是 ( )
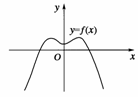
图1


解析:y=f(x)的单调变化情况为增、减、增、减,
因此y=f′(x)的符号变化情况为大于零、小于零、大于零、小于零.故选A.
答案:A

图2
2.若函数f(x)=(k-1)ax-a-x(a>0且a≠1)在R上既是奇函数,又是减函数,则g(x)=loga(x+k)的图象是 ( )

解析:由函数f(x)=(k-1)ax-a-x(a>0且a≠1)在R上为奇函数知,k-1=1,即k=2.
又f(x)为减函数,∴0<a<1.
∴g(x)=loga(x+2)(0<a<1).
答案:A
1.函数f(x)= -x的图象关于 ( )
A.y轴对称 B.直线y=-x对称
C.坐标原点对称 D.直线y=x对称
∵f(x)=-f(-x),∴f(x)=-x是奇函数.
∴f(x)的图象关于坐标原点对称. www.k@s@5@ 高#考#资#源#网
答案:C
12. 已知定义在R上的奇函数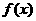 ,满足
,满足 ,且在区间[0,2]上是增函数,则( ).
,且在区间[0,2]上是增函数,则( ). 

A.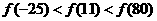 B.
B. 
C.  D.
D. 
11.在区间 上随机取一个数x,
上随机取一个数x, 的值介于0到
的值介于0到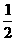 之间的概率为( ).
之间的概率为( ).
A. B.
B. C.
C.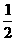 D.
D.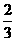


10. 设斜率为2的直线 过抛物线
过抛物线 的焦点F,且和
的焦点F,且和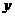 轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为( ).
轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为( ).


A. B.
B. C.
C.  D.
D. 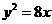
9. 已知α,β表示两个不同的平面,m为平面α内的一条直线,则“ ”是“
”是“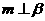 ”的(
)
”的(
)
A.充分不必要条件 B.必要不充分条件
C.充要条件
D.既不充分也不必要条件 

8.设P是△ABC所在平面内的一点, ,则( )
,则( )
A. B.
B. 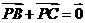
C.
 D.
D.
7. 定义在R上的函数f(x)满足f(x)=
定义在R上的函数f(x)满足f(x)=  ,则f(3)的值为( )
,则f(3)的值为( )
A.-1 B. -2 C.1 D. 2
6. 函数 的图像大致为( ).
的图像大致为( ). 


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com