7．对于集合A＝{x|x²－x－6≤0}和B＝{x||x－a|≤1}，若A∩B＝B，则实数a的取值范围是__________．

解析：A＝{x|－2≤x≤3}

B＝{x|a－1≤x≤a+1}

由A∩B＝B　有B⊆A.

∴a－1≥－2且a+1≤3.

解得－1≤a≤2.

答案：[－1,2]

6．f(x)＝6x³+9x+1，若f(a)+f(a－1)>2，则a的取值范围为　　　　　　　　　　　　　 (　)

A．a>　 　　　　　　　　　　　　　 B．a<1

C．a>0　 　　　　　　　　　　　　　 D．0<a<1

解析：f(a)+f(a－1)>2⇔f(a)－1>－[f(a－1)－1]，

令F(x)＝f(x)－1＝6x³+9x，

则有F(x)为奇函数且为增函数，

所以有F(a)>F(1－a)⇔a>1－a⇒a>.

答案：A

5．(2010·北京东城一模)函数y＝f(x)的图象是圆心在原点的单位圆的两段弧(如图3)，则不等式f(x)<f(－x)+2x的解集为　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．{x|－<x<0或<x≤1}

B．{x|－1≤x<－或<x≤1}

C．{x|－1≤x<－或0<x<}

D．{x|－<x<且x≠0}

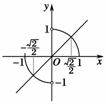
图4

解析：f(x)＝该函数f(x)是奇函数．

由f(x)<f(－x)+2x，得f(x)<x.

作直线y＝x，满足f(x)<x的x如图4所示：

∴－<x<0或<x≤1.

答案：A

4．已知函数f(x)为偶函数，在(－∞，0]上为减函数，并且f(6)＝0，则不等式xf(x)<0的解集为　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．(－∞，－6)∪(6，+∞)

B．(－∞，－6)∪(0,6)

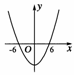
图2

C．(－6,0)∪(6，+∞)

D．(－6,6)

解析：∵f(x)为偶函数且在(－∞，0]上为减函数，

∴在[0，+∞)上为增函数，作f(x)的大致图象，如图2，

由图可得xf(x)<0的解集为(－∞，－6)∪(0,6)．

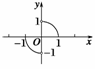
图3

答案：B

3．已知向量a＝(x，－1)与向量b＝(1，)，则不等式a·b≤0的解集为　　　　　　 (　)

A．{x|x≤－1或x≥1}

B．{x|－1≤x<0或x≥1}

C．{x|x≤－1或0≤x≤1}

D．{x|x≤－1或0<x≤1}

解析：a·b＝x－，

由x－≤0⇒≤0⇒≤0.

∴x≤－1或0<x≤1.

答案：D

2．若a>0，b>0，则不等式－b<<a等价于　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．－<x<0或0<x<

B．－<x<

C．x<－或x>

D．x<－或x>

解析：即当a>0，b>0时解不等式－b<<a

⇔⇔

⇔⇔

利用数轴：

图1

可得x>或x<－.

答案：D

1．不等式≥2的解集为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．[－1,0)　　　　 B．[－1，+∞)

C．(－∞，－1]　 　　　　　　　 D．(－∞，－1]∪(0，+∞)

解析：∵≥2，∴－2≥0，即≤0，解得－1≤x<0.

答案：A

13．(20分)(2009·江苏高考)按照某学者的理论，假设一个人生产某产品的单件成本为a元，如果他卖出该产品的单价为m元，则他的满意度为；如果他买进该产品的单价为n元，则他的满意度为.如果一个人对两种交易(卖出或买进)的满意度分别为h₁和h₂，则他对这两种交易的综合满意度为.

现假设甲生产A，B两种产品的单件成本分别为12元和5元，乙生产A，B两种产品的单件成本分别为3元和20元．设产品A、B的单价分别为m_A元和m_B元，甲买进A与卖出B的综合满意度为h_甲，乙卖出A与买进B的综合满意度为h_乙．

(1)求h_甲和h_乙关于m_A、m_B的表达式；当m_A＝m_B时，求证：h_甲＝h_乙；

(2)设m_A＝m_B，当m_A、m_B分别为多少时，甲、乙两人的综合满意度均最大？最大的综合满意度为多少？

(3)记(2)中最大的综合满意度为h₀，试问能否适当选取m_A、m_B的值，使得h_甲≥h₀和h_乙≥h₀同时成立，但等号不同时成立？试说明理由．

解：设m_A＝x，m_B＝y.

(1)甲买进产品A的满意度：h_1甲＝；甲卖出产品B的满意度：h_2甲＝；

甲买进产品A和卖出产品B的综合满意度：

h_甲＝；

同理，乙卖出产品A和买进产品B的综合满意度：

h_乙＝.

当x＝y时，h_甲＝＝＝，h_乙＝＝＝，

故h_甲＝h_乙．

(2)当x＝y时，由(1)知h_甲＝h_乙＝，

因为＝≤，且等号成立当且仅当y＝10.

当y＝10时，x＝6.

因此，当m_A＝6，m_B＝10时，甲、乙两人的综合满意度均最大，且最大的综合满意度为.

(3)由(2)知h₀＝.

因为h_甲h_乙＝

＝≤，

所以，当h_甲≥，h_乙≥时，有h_甲＝h_乙＝.

因此，不能取到m_A，m_B的值，使得h_甲≥h₀和h_乙≥h₀同时成立，但等号不同时成立．

12．(15分)某商品每件成本9元，售价30元，每星期卖出432件，如果降低价格，销售量可以增加，且每星期多卖出的商品件数与商品单价的降低值x(单位：元，0≤x≤21)的平方成正比．已知商品单价降低2元时，一星期多卖出24件．

(1)将一个星期的商品销售利润表示成x的函数；

(2)如何定价才能使一个星期的商品销售利润最大？

解：(1)设商品降价x元，则多卖的商品数为kx²，若记商品在一个星期的获利为f(x)，则依题意有f(x)＝(30－x－9)(432+kx²)＝(21－x)(432+kx²)．

又由已知条件，24＝k·2²，于是有k＝6，所以f(x)＝－6x³+126x²－432x+9072，x∈[0,21]．

(2)根据(1)，我们有f′(x)＝－18x²+252x－432

＝－18(x－2)(x－12)，

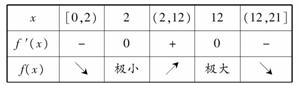
故x＝12时，f(x)达到极大值，因为f(0)＝9072，f(12)＝11664，所以定价为30－12＝18元能使一个星期的商品销售利润最大．

11．(15分)某公司拟投资100万元，有两种获利的方式可供选择：一种是年利率10%，按单利计算，5年后收回本金和利息；另一种是年利率9%，按每年复利一次计算，5年后收回本金和利息．哪一种投资更有利？这种投资比另一种投资5年可多得利息多少元？

解：本金100万元，年利率10%，按单利计算，5年后的本息和是100×(1+10%×5)＝150(万元)．

本金100万元，年利率9%，按每年复利一次计算，5年后的本息和是100×(1+9%)⁵＝153.86(万元)．

由此可见，按年利率9%每年复利一次计算的要比年利率10%单利计算的更有利，5年后可多得利息3.86万元．