4．已知0<a<1，b>1且ab>1，则下列不等式中成立的是　　　　　　　　　　　　　　　　　 (　)

A．log_b<log_ab<log_a

B．log_ab<log_b<log_a

C．log_ab<log_a<log_b

D．log_a<log_ab<log_ba

解析：特殊值法．令a＝，b＝100.

答案：B

3．某商品计划提价，现有四种方案：方案(Ⅰ)先提价m%，再提价n%；方案(Ⅱ)先提价n%，再提价m%；方案(Ⅲ)分两次提价，每次提价()%；方案(Ⅳ)一次性提价(m+n)%，已知m>n>0，那么四种提价方案中，哪一种提价最多　　　 　　　　　　　　　　　　　　　　　　　　　 (　)

A．Ⅰ　 　　　　　　　　　　　　　　 B．Ⅱ

C．Ⅲ　 　　　　　　　　　　　　　　 D．Ⅳ

解析：设提价前的价格为p，则：

方案(Ⅰ)：p(1+m%)(1+n%)；

方案(Ⅱ)：p(1+n%)(1+m%)；

方案(Ⅲ)：p(1+%)²；

方案(Ⅳ)：p[1+(m+n)%]．比较这四个值，(Ⅰ)，(Ⅱ)相同，且(1+%)²＝1+(m+n)%+(%)²>(1+n%)(1+m%)＝1+(m+n)%+m%·n%>1+(m+n)%，故方案(Ⅲ)提价最多．故选C.

答案：C

2．设a>2，b>2，则　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．ab>a+b

B．ab<a+b

C．存在a，b，使得ab＝a+b

D.>1

解析：⇒ab>2(a+b)－4>a+b.

答案：A

1．已知P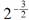＝，Q＝()³，R＝()³，则P、Q、R的大小关系是　　　　　　　　　　 (　)

A．P<Q<R　　　　　 B．R<P<Q

C．Q<P<R　 　　　　　　　　　　　 D．R<Q<P

解析：∵0<P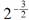＝<1，Q＝()³>1,0<R＝()³＝<1，

∴P<Q，R<Q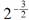，∵ >2^－3.

∴R<P，∴R<P<Q.

答案：B

13．(20分)(2009·乐山二次调研)已知函数f(x)＝kx+b(k≠0)的图象与x，y轴分别相交于点A、B，＝2i+2j(i、j分别是与x、y轴正半轴同方向的单位向量)，函数g(x)＝x²－x+a－2(a∈R)．

(1)求实数k、b的值；

(2)若不等式≤1的解集为(－∞，－2)∪[－1,3]，求a的值．

解：(1)由题知A(－，0)，B(0，b)∴＝(，b)

由＝2i+2j＝(2,2)，∴

∴k＝1，b＝2，∴f(x)＝x+2

(2)＝≤1，

∴≤0

∵其解集为(－∞，－2)∪[－1,3]，

∴－1,3是方程x²－2x+a－2＝0的两根

∴a－2＝－3，∴a＝－1.

12．(15分)已知不等式x²－3x+t<0的解集为{x|1<x<m，x∈R}．

(1)求t，m的值；

(2)若函数f(x)＝－x²+ax+4在区间(－∞，1]上递增，求关于x的不等式log_a(－mx²+3x+2－t)<0的解集．

解：(1)∵不等式x²－3x+t<0的解集为{x|1<x<m，x∈R}，∴，得.

(2)∵f(x)＝－(x－)²+4+在(－∞，1]上递增，

∴≥1，a≥2.

又log_a(－mx²+3x+2－t)＝log_a(－2x²+3x)<0.

由a≥2，可知0<－2x²+3x<1.

由2x²－3x<0，得0<x<，

由2x²－3x+1>0，得x<或x>1.

∴不等式的解集为{x|0<x<或1<x<}．

11．(15分)已知k<1，求不等式>1的解集．

解：把原不等式移项通分得>0，

由k<1⇒k－1<0，则可整理得<0.(※)

当>2，即0<k<1时，由(※)得2<x<；

当＝2，即k＝0时，由(※)得x∈Ø；

当<2，即k<0时，由(※)得<x<2.

综上，当k<0时，原不等式的解集为(，2)；

当k＝0时，原不等式无解；

当0<k<1时，原不等式的解集为(2，)．

10．(2009·合肥质检二)若a+1>0，则不等式x≥的解集为________．

解析：原不等式可变形为≥0⇔(x+a)(x－1)≥0且x－1≠0解得x∈(－∞，－a]∪(1，+∞)．

答案：(－∞，－a]∪(1，+∞)

9．关于x的不等式>a(其中a>0，b>0，c<0)的解集为________．

解析：原不等式可化为<0，

即(x－b)(x－b+)<0.

又<0，∴b<b－，

∴b<x<b－，

∴原不等式的解集是(b，b－)．

答案：(b，b－)

8．若规定\o(\s\up7(ac＝|ad－bc|，则不等式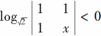的解集为__________．

解析：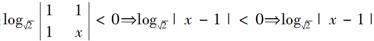

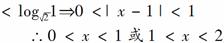
答案：(0,1)∪(1,2)