12．(15分)设f(x)＝1+log_x3，g(x)＝2log_x2，其中x>0，且x≠1，试比较f(x)与g(x)的大小．

解：f(x)－g(x)＝(1+log_x3)－2log_x2＝log_x.

∵对数值的正负与底数和真数与1的大小有关，

∴需分情况讨论．

①当或，

故1<x<时，log_x<0，∴f(x)<g(x)；

②当＝1，即x＝时，log_x＝0，

故f(x)＝g(x)；

③当或，

即0<x<1或x>时，log_x>0，

故f(x)>g(x)．

综上所述，当1<x<时，f(x)<g(x)；

当x＝时，f(x)＝g(x)；

当0<x<1或x>时，f(x)>g(x)．

11．(15分)已知a∈R，a≠1，比较与1+2a+a²的大小．

解：∵－(1+2a+a²)＝

∴①当a＝0或a＝±时，＝1+2a+a²；

②当a<－或a>时，<1+2a+a²；

③当－<a<且a≠1，a≠0时，>1+2a+a².

10．(2009·江苏苏州二模)设a>b>c>0，x＝，y＝，z＝，则x，y，z的大小顺序是__________．

解析：令a＝3，b＝2，c＝1，则x＝，y＝，z＝，故z>y>x.

答案：z>y>x

9．已知－1≤a+b≤1,1≤a－b≤3，则3a－b的取值范围是________．

解析：将3a－b用a+b和a－b表示，

设3a－b＝m(a+b)+n(a－b)＝(m+n)a+(m－n)b.

比较系数，得

∴3a－b＝(a+b)+2(a－b)．

又－1≤a+b≤1,1≤a－b≤3，

∴1≤3a－b≤7.

答案：[1,7]

8．设a＝2－，b＝－2，c＝5－2，则a、b、c之间的大小关系为__________．

解析：a＝2－＝－<0.∴b>0.

c＝5－2＝－>0.

b－c＝3－7＝－<0.

∴c>b>a.

答案：c>b>a

7．若a<b<0，则与的大小为________．

解析：由a<b<0可得a<a－b<0.

答案：<

6．(2009·合肥质检三)设a>0，b>0，c>0，下列不等关系不恒成立的是　　　　　　 (　)

A．c³+c+1>c²+c－1

B．|a－b|≤|a－c|+|b－c|

C．若a+4b＝1，则+>6.8

D．ax²+bx－c≥0(x∈R)

解析：只有满足a>0且Δ＝b²+4ac≤0时D中不等式才恒成立，故选D.

答案：D

4．(2009·山东威海二模)设a，b，c，d∈R⁺，且a+d＝b+c，|a－d|<|b－c|，则(　)

A．ad＝bc　 　　　　　　　　　　　 　B．ad<bc

C．ad>bc　 　　　　　　　　　　　　 　D．ad≤bc

解析：将两条件平方，得

由②－①得－4ad<－4bc，∴ad>bc.

答案：C

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　 (　)

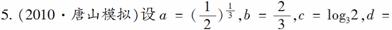
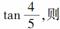A．d>a>b>c　 　　　　　　　　　　 　B．d>c>b>a

C．d>b>c>a　 　　　　　　　　　　 　D．a>c>b>d

解析：由题知，d>tan＝1，而a、b、c均小于1.

故d最大，而a³＝，b³＝，∴a>b；

答案：A

3．设0<b<a<1，则下列不等式成立的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

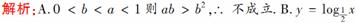
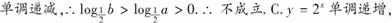
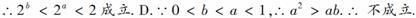
答案：C

2．设a+b<0，且a>0，则下列不等式成立的是　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．a²<b²<－ab　 　　　　　　　　 　B．b²<－ab<a²

C．a²<－ab<b²　 　　　　　　　　 　D．－ab<b²<a²

解析：令a＝1，b＝－2即可．故选C.

答案：C