13．(20分)(2009·山东青岛模拟)已知二次函数f(x)对于任意x∈R，都有f(1－x)＝f(1+x)成立，设向量a＝(sinθ，2)，b＝(2sinθ，)，c＝(cos2θ，1)，d＝(1,2)，当θ∈[0，π]时，求不等式f(a·b)>f(c·d)的解集．

解：∵f(1－x)＝f(1+x)，

∴f(x)的对称轴为x＝1，

∵a·b＝2sin²θ+1≥1，c·d＝cos2θ+2≥1，

不妨设f(x)的二次项系数为m，

①当m>0时，f(x)在[1，+∞)上为增函数，

由f(a·b)>f(c·d)得2sin²θ+1>cos2θ+2，

∴cos2θ<0.∵θ∈[0，π]，

∴<θ<.

②当m<0时，f(x)在[1，+∞)上为减函数，

则2sin²θ+1<cos2θ+2，∴cos2θ>0.

∴0≤θ<或<θ≤π.

∴当二次项系数为m>0时，原不等式的解集为(，)　 www.k@s@5@　　　　　　　　　　　　　 　高#考#资#源#网

当二次项系数m<0时，原不等式的解集为[0，)∪(π，π]．

12．(15分)(2009·广东高考)已知向量a＝(sinθ，－2)与b＝(1，cosθ)互相垂直，其中θ∈(0，)．

(1)求sinθ和cosθ的值；

(2)若sin(θ－φ)＝，0<φ<，求cosφ的值．

解：(1)∵a⊥b，则a·b＝sinθ－2cosθ＝0，即sinθ＝2cosθ，代入sin²θ+cos²θ＝1，得sinθ＝±，cosθ＝±，又θ∈(0，)，∴sinθ＝，cosθ＝.

(2)∵0<φ<，0<θ<，∴－<θ－φ<.

则cos(θ－φ)＝＝，

∴cosφ＝cos[θ－(θ－φ)]＝cosθcos(θ－φ)+sinθsin(θ－φ)＝.

11．(15分)已知α为锐角，cosα＝，tan(α－β)＝，求tanα和tanβ的值．

解：∵cosα＝，且α为锐角，

∴sinα＝＝＝.

∴tanα＝＝.

于是tanβ＝tan[α－(α－β)]

＝＝＝.

10．(2009·西城抽样)给出下列四个函数：

①y＝sinx+cosx；②y＝sinx－cosx；

③y＝sinx·cosx；④y＝.

其中在(0，)上既无最大值也无最小值的函数是______．

解析：对于①，注意到当x∈(0，)时，函数y＝sinx+cosx＝sin(x+)有最大值；对于②，注意到当x∈

(0，)时，x－∈(－，)，sin(x－)∈(－，)，此时y＝sinx－cosx＝sin(x－)既无最大值也无最小值；对于③，注意到当x∈(0，)时，2x∈(0，π)，此时函数y＝sinxcosx＝sin2x有最大值；对于④，当x∈(0，)时，y＝＝tanx是增函数，此时该函数既无最大值也无最小值．综上所述，其中在(0，)上既无最大值也无最小值的函数是②④.

答案：②④

9．(2010·东城目标检测)已知{a_n}为等差数列，若a₁+a₅+a₉＝π，则cos(a₂+a₈)的值为__________．

解析：由a₁+a₅+a₉＝π，得a₅＝，a₂+a₈＝2a₅＝，

∴cos(a₂+a₈)＝－.

答案：－

8．已知△ABC的三个内角A、B、C 满足cosA(sinB+cosB)+cosC＝0，则∠A＝________.

解析：由题意得cosA(sinB+cosB)－cos(A+B)＝0，展开并整理得sinB(cosA+sinA)＝0，又sinB>0，因此cosA+sinA＝0，tanA＝－1，又A∈(0，π)，因此∠A＝.

答案：(或135°)

7．计算＝________.

解析：sin(α+30°)+cos(α+60°)＝sinα+cosα+cosα－sinα＝cosα，则所求答案为.

答案：

6．(2010·衡阳联考)如图1，小正六边形沿着大正六边形的边，按顺时针方向滚动，小正六边形的边长是大正六形边长的一半，如果小正六边形沿着大正六边形的边滚动一周后返回出发时的位置，在这个过程中向量围绕着点O旋转了θ角，其中O为小正六边形的中心，则sin+cos的值是

(　)

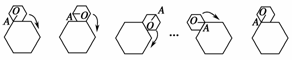　 www.k@s@5@　　　　　　　　　　　　　　 高#考#资#源#网

图1

A．1　 　　　　　　　　　　　　　　　　　　　 B.

C．－1　 　　　　　　　　　　　　　　　　　 D．－

解析：结合图形易知θ＝6π，∴sin+cos＝－1.

答案：C

5．已知方程x²+4ax+3a+1＝0(a>0)的两根为tanα、tanβ，且α，β∈(－，)，则tan的值是

(　)

A.　 　　　　　　　　　　　　　　　　　　　　 B．－2

C.　 　　　　　　　　　　　　　　　　　　　　 D.或－2

解析：∵a>0，∴tanα+tanβ＝－4a<0，tanα·tanβ＝3a+1>0，α、β∈(－，)，∴α、β∈(－，0)，则∈(－，0)，又tan(α+β)＝＝＝，∴tan(α+β)＝＝，整理得2tan²+3tan－2＝0，解得tan＝－2，故选B.

答案：B

4．已知sinαsinβ＝1，则cos(α－β)的值为

(　)

A．1　 　　　　　　　　　　　　　　　　　　　 B．0

C．－1　 　　　　　　　　　　　　　　　　　 D．1或－1

解析：由|sinα|≤1，|sinβ|≤1及sinαsinβ＝1可得cosαcosβ＝0，于是cos(α－β)＝cosαcosβ+sinαsinβ＝1.

答案：A