
题目列表(包括答案和解析)
4. 在边长为a的正三角形的三个角处各剪去一个四边形.这个四边形是由两个全等的直角三角形组成的,并且这三个四边形也全等,如图①.若用剩下的部分折成一个无盖的正三棱柱形容器,如图②.则当容器的高为多少时,可使这个容器的容积最大,并求出容积的最大值.
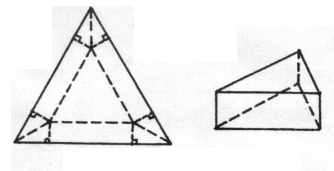
图① 图②
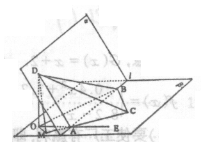
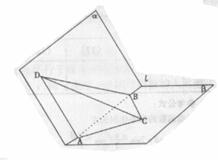
3. 如图a-l-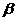 是120°的二面角,A,B两点在棱上,AB=2,D在
是120°的二面角,A,B两点在棱上,AB=2,D在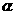 内,三角形ABD是等腰直角三角形,∠DAB=90°,C在
内,三角形ABD是等腰直角三角形,∠DAB=90°,C在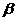 内,
内,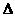 ABC是等腰直角三角形∠ACB=
ABC是等腰直角三角形∠ACB=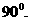
(I) 求三棱锥D-ABC的体积;
(2)求二面角D-AC-B的大小;
(3)求异面直线AB、CD所成的角.
1. 四棱锥P-ABCD的底面是边长为a的正方形,PB⊥面ABCD.
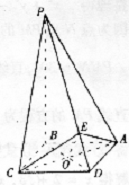 (1)若面PAD与面ABCD所成的二面角为60°,求这个四棱锥的体积;
(1)若面PAD与面ABCD所成的二面角为60°,求这个四棱锥的体积;
(2)证明无论四棱锥的高怎样变化,面PAD与面PCD所成的二面角恒大于90°
2 如图,直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,∠ACB=900,AC=1,C点到AB1的距离为CE=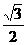 ,D为AB的中点.
,D为AB的中点.
(1)求证:AB1⊥平面CED;
(2)求异面直线AB1与CD之间的距离;
 (3)求二面角B1-AC-B的平面角.
(3)求二面角B1-AC-B的平面角.
25. 某城市2001年末汽车保有量为30万辆,预计此后每年报废上一年末汽车保有量的6%,并且每年新增汽车数量相同。为了保护城市环境,要求该城市汽车保有量不超过60万辆,那么每年新增汽车数量不应超过多少辆?
24. 己知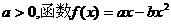 ,
,
(1)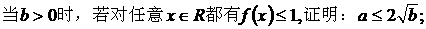
(2)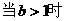 ,证明:对任意
,证明:对任意 ,
,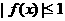 的充要条件是
的充要条件是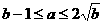 ;
;
(3)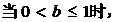 讨论:对任意
讨论:对任意 ,
,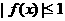 的充要条件。
的充要条件。
23. 已知函数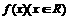 满足下列条件:对任意的实数x1,x2都有
满足下列条件:对任意的实数x1,x2都有
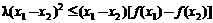
和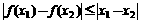 ,其中
,其中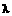 是大于0的常数.
是大于0的常数.
设实数a0,a,b满足
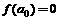 和
和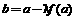
(Ⅰ)证明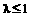 ,并且不存在
,并且不存在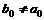 ,使得
,使得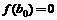 ;
;
(Ⅱ)证明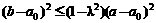 ;
;
(Ⅲ)证明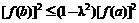 .
.
22. 已知实数a,b,c满足条件: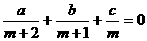 ,其中m是正数,对于f(x)=ax2+bx+c
,其中m是正数,对于f(x)=ax2+bx+c
(1)如果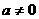 ,证明:
,证明:
(2)如果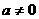 ,证明:方程f(x)=0在(0,1)内有解。
,证明:方程f(x)=0在(0,1)内有解。
21. (1)设a>0,b>0且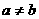 ,试比较aabb与abba的大小。
,试比较aabb与abba的大小。
(2)已知函数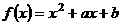 ,
,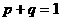 ,试比较
,试比较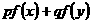 与
与 的大小.
的大小.
20.已知函数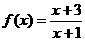 ,数列
,数列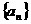 满足:
满足: ,
,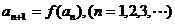
(1)设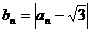 证明:
证明: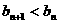 (2)证明:
(2)证明: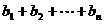

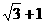
19.设函数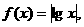 正实数
正实数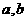 满足
满足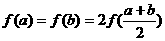 ,且
,且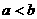
(1)求证: ;
(2)求证:
;
(2)求证: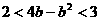
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com