
题目列表(包括答案和解析)
2.对两个变量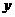 与
与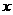 进行线性回归分析,分别选择了
进行线性回归分析,分别选择了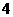 个不同的模型,它们的相关系数
个不同的模型,它们的相关系数 如下,其中拟合程度最好的模型是 (
)
如下,其中拟合程度最好的模型是 (
)
A
.模型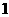 的相关系数
的相关系数 为
为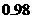 B.
模型
B.
模型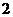 的相关系数
的相关系数 为
为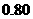
C.
模型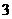 的相关系数
的相关系数 为
为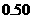 D.
模型
D.
模型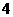 的相关系数
的相关系数 为
为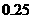
1.下列说法中错误的是 ( )
A.如果变量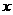 与
与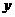 之间存在着线性相关关系,则我们根据试验数据得到的点
之间存在着线性相关关系,则我们根据试验数据得到的点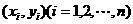 将散布在某一条直线的附近
将散布在某一条直线的附近
B.如果两个变量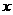 与
与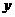 之间不存在着线性关系,那么根据它们的一组数据
之间不存在着线性关系,那么根据它们的一组数据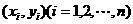 不能写出一个线性方程
不能写出一个线性方程
C.设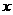 ,
,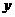 是具有相关关系的两个变量,且
是具有相关关系的两个变量,且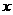 关于
关于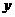 的线性回归方程为
的线性回归方程为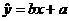 ,
,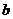 叫做回归系数
叫做回归系数
D.为使求出的线性回归方程有意义,可用统计检验的方法来判断变量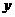 与
与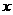 之间是否存
之间是否存
在线性相关关系
(1)定理的表示形式: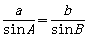
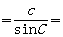
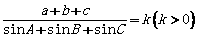 ;
;
或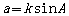 ,
,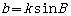 ,
,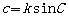
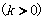
(2)正弦定理的应用范围:
①已知两角和任一边,求其它两边及一角;
②已知两边和其中一边对角,求另一边的对角。
[探索研究]
在初中,我们已学过如何解直角三角形,下面就首先来探讨直角三角形中,角与边的等式关系。如图,在Rt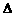 ABC中,设BC=a,AC=b,AB=c, 根据锐角三角函数中正弦函数的定义,
ABC中,设BC=a,AC=b,AB=c, 根据锐角三角函数中正弦函数的定义,
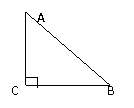 有
有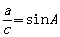 ,
,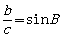 ,又
,又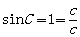 ,
,
则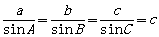
从而在直角三角形ABC中,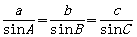
思考1:那么对于任意的三角形,以上关系式是否仍然成立?(由学生讨论、分析)
可分为锐角三角形和钝角三角形两种情况:
 如图1.1-3,(1)当
如图1.1-3,(1)当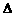 ABC是锐角三角形时,设边AB上的高是CD,根据任意角三角函数的定义,
ABC是锐角三角形时,设边AB上的高是CD,根据任意角三角函数的定义,
有CD=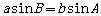 ,则
,则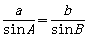 ,
C
,
C
同理可得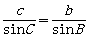 ,
b
a
,
b
a
 从而
从而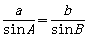
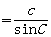 A
c B
A
c B
(2)当 ABC是钝角三角形时,以上关系式仍然成立。(由学生课后自己推导)
ABC是钝角三角形时,以上关系式仍然成立。(由学生课后自己推导)
思考2:还有其方法吗?
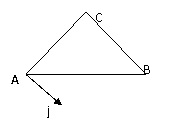
由于涉及边长问题,从而可以考虑用向量来研究这问题。
(证法二):过点A作单位向量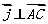 , 由向量的加法可得
, 由向量的加法可得 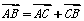
则 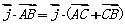
 ∴
∴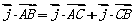
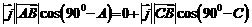
∴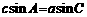 ,即
,即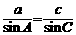
同理,过点C作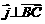 ,可得
,可得 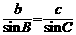 从而
从而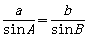
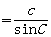
从上面的研探过程,可得以下定理
正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,即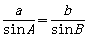
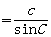
[理解定理]
(1)正弦定理说明同一三角形中,边与其对角的正弦成正比,且比例系数为同一正数,
即存在正数k使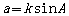 ,
,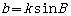 ,
,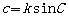 ;
;
(2)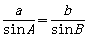
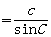 等价于
等价于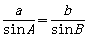 ,
,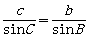 ,
,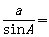
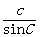
思考:正弦定理的基本作用是什么?
①已知三角形的任意两角及其一边可以求其他边,如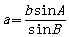 ;
;
②已知三角形的任意两边与其中一边的对角可以求其他角的正弦值,如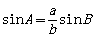 。
。
一般地,已知三角形的某些边和角,求其他的边和角的过程叫作解三角形。
[例题分析]
例1.在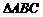 中,已知
中,已知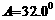 ,
,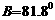 ,
,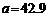 cm,解三角形。
cm,解三角形。
解:根据三角形内角和定理,
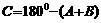
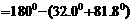
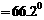 ;
;
根据正弦定理,
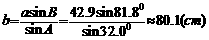 ;
;
根据正弦定理, 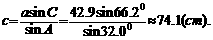
评述:对于解三角形中的复杂运算可使用计算器。
练习:在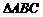 中,已知下列条件解三角形。
中,已知下列条件解三角形。
(1)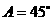 ,
,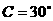 ,
,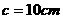 , (2)
, (2) ,
, ,
,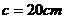
例2. 在 中,已知
中,已知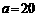 cm,
cm,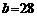 cm,
cm,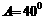 ,解三角形(角度精确到
,解三角形(角度精确到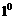 ,边长精确到1cm)。
,边长精确到1cm)。
解:根据正弦定理,
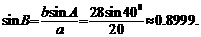 因为
因为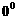 <
<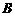 <
<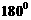 ,所以
,所以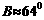 ,或
,或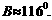
⑴ 当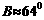 时,
时,  ,
,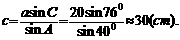
⑵ 当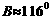 时,
时,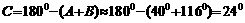 ,
,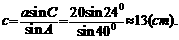
应注意已知两边和其中一边的对角解三角形时,可能有两解的情形。
课堂练习
第4页练习第2题。
思考题:在 ABC中,
ABC中,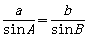
 ,这个k与
,这个k与 ABC有什么关系?
ABC有什么关系?
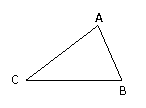 如图1.1-1,固定
如图1.1-1,固定 ABC的边CB及
ABC的边CB及 B,使边AC绕着顶点C转动。
B,使边AC绕着顶点C转动。
思考: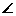 C的大小与它的对边AB的长度之间有怎样的数量关系?
C的大小与它的对边AB的长度之间有怎样的数量关系?
显然,边AB的长度随着其对角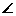 C的大小的增大而增大。
C的大小的增大而增大。
能否用一个等式把这种关系精确地表示出来?
10.已知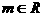 ,直线
,直线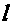 :
: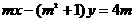 和圆C:
和圆C: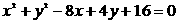
(1)求直线 斜率的取值范围;
斜率的取值范围;
(2) 直线 能否将圆C分割成弧长的比值为
能否将圆C分割成弧长的比值为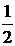 的两段圆弧?为什么?
的两段圆弧?为什么?
*11.已知与曲线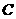 :
: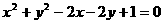 相切的直线
相切的直线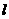 交
交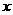 轴、
轴、 轴于
轴于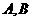 两点,
两点, 为原点,
为原点,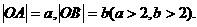 (1)求证:
(1)求证: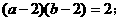
(2)求线段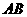 中点的轨迹方程; ⑶求
中点的轨迹方程; ⑶求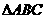 面积的最小值.
面积的最小值.
9.设圆上的点 (2,3)关于直线
(2,3)关于直线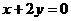 的对称点仍在这个圆上,且与直线
的对称点仍在这个圆上,且与直线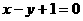 相交的弦长为
相交的弦长为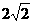 ,求圆的方程。
,求圆的方程。
7.动圆与两定圆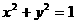 和
和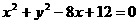 都外切,则动圆圆心的轨迹为__________________.
都外切,则动圆圆心的轨迹为__________________.
*8. 已知圆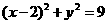 和直线
和直线 交于A,B两点,O是坐标原点, 若
交于A,B两点,O是坐标原点, 若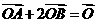 ,则
,则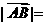 .
.
6.一动点在圆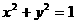 上移动时,它与定点
上移动时,它与定点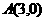 连线中点的轨迹方程是____________.
连线中点的轨迹方程是____________.
5.直线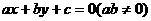 ,截圆
,截圆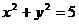 所得弦长等于4,则以|
所得弦长等于4,则以|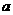 |、|
|、|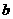 |、|
|、|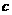 |为边长的三角形的形状一定是______________________.
|为边长的三角形的形状一定是______________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com