8．从装有个红球和个白球的口袋内任取个球，那么互斥而不对立的两个事件是(　　 )A．至少有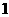个白球；都是白球　　　　　　　　　　　　　　　　　　 B．至少有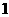个白球；至少有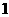个红球

　　　　 C．恰有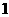个白球；恰有个白球　　　　　　　　　 D．至少有一个白球；都是红球

7．在天气预报中，有“降水概率预报”，例如预报“明天降水概率为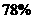”，这是指(　　 )

　　　　 A．明天该地区有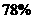的地区降水，其他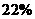的地区不降水

　　　　 B．明天该地区约有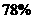的时间降水，其他时间不降水

　　　　 C．气象台的专家中，有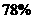的人认为会降水，另外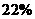的专家认为不降水

　　　　 D．明天该地区的降水的可能性为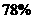

6．若在同等条件下进行次重复试验得到某个事件发生的频率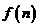，则随着的逐渐增加，有　　　　　　 　　　　 　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　　 A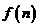．与某个常数相等

　　　　 B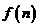．与某个常数的差逐渐减小

　　　　 C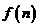．与某个常数差的绝对值逐渐减小

　　　　 D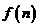．在某个常数附近摆动并趋于稳定

5．在件同类产品中，其中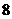件为正品，件为次品．从中任意抽出件的必然事件是(　　 )

　　　　 A．件都是正品　　　　　　　　　　　　　　　　　　　　　　　　 B．至少有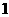件是次品

　　　　 C．件都是次品　　　　　　　　　　　　　　　　　　　　　　　　 D．至少有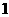件是正品

4．从鱼塘捕得同时放养的鲤鱼尾，从中任选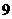尾，称得每尾鱼的质量分别是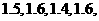 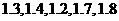(单位：千克)．依此估计这尾鱼的总质量大约是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　　 A．千克　　　　　　　　 B．千克　　　　　　　　 C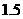．千克　　　　　　　　　 D．千克

3．在个零件中，有一级品个，二级品个，三级品个，从中抽取个作为样本，有以下三种抽样方法：

　　　　 ①采用随机抽样法，将零件编号为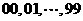，抽签取出个；

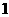　　　　 ②采用系统抽样法，将所有零件分成组，每组个，然后每组随机抽取个；

　　　　 ③采用分层抽样法，从一级品中随机抽取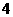个，从二级品中随机抽取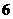个，从三级品中随机抽取个．

　　　　 则下述判断中正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　　 A．不论采用何种抽样方法，这个零件中每个被抽到的可能性均为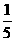

　　　　 B．①、②两种抽样方法，这个零件中每个被抽到的可能性均为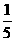；③并非如此

　　　　 C．①、③两种抽样方法，这个零件中每个被抽到的可能性均为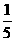；②并非如此

　　　　 D．采用不同的抽样方法，这个零件中每个被抽到的可能性是各不相同的

2．　 ①教育局督学组到学校检查工作，需在高三年级的学号为001·800的学生中抽调人参加关于学校管理的综合座谈；

　　　　 ②该校高三年级这名学生期中考试的数学成绩有160在120分以上(包括分)，480人在120以下90分以上(包括90分)，其余的在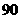分以下，现欲从中抽出人研讨进一步改进数学教和学的座谈；

　　　　 ③该校高三年级这800名学生参加2010年元旦聚会，要产生20名“幸运之星”．

　　　　 以上三件事，合适的抽样方法依次为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　　 A．系统抽样，分层抽样，系统抽样

　　　　 B．系统抽样，系统抽样，简单随机抽样

　　　　 C．分层抽样，简单随机抽样，简单随机抽样

　　　　 D．系统抽样，分层抽样，简单随机抽样

1．要从已编号(1·50)的枚最新研制的某型号导弹中随机抽取枚来进行发射试验，用每部分选取的号码间隔一样的系统抽样方法确定所选取的枚导弹的编号可能是(　 )

　　　　 A．5,10,15,20,25　　　　　　　　　　　　　　　　　　　　　　　　　 B．3,13,23,33,43

　　　　 C．1,2,3,4,5　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．2,4,8,16,32

22．(14分)

设椭圆E: 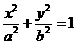(a,b>0)过M(2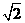，) ，N(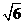,1)两点，O为坐标原点．

　 (Ⅰ)求椭圆E的方程；

　 (Ⅱ)是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆E恒有两个交点A,B,

　　　　 且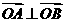？若存在，写出该圆的方程，并求|AB |的取值范围，若不存在说明理

21．(12分)如图，已知椭圆的中心在原点，焦点在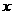轴上，长轴长是短轴长的2倍且经过点M(2,1)，平行于OM的直线l在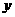轴上的截距为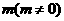，l交椭圆于A、B两个不同点．

　 (1)求椭圆的方程；

　 (2)求m的取值范围；

　 (3)求证直线MA、MB与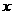轴始终围成一个等腰三角形．