
题目列表(包括答案和解析)
2.若a<0<b,则在不等式:①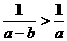 ,②
,②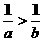 ,③|a|>|b|,④
,③|a|>|b|,④ 中不能成立的是_________________________
中不能成立的是_________________________
1.“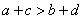 ”是“
”是“ 且
且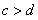 ”的 ______________________条件
”的 ______________________条件
2.前n行共有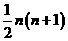 个“合格数”数.
个“合格数”数.
题目已经暗示:2010一定是“合格数”,设2010位于这张表的
第n行,那么: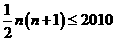 ,即
,即
|
|
 ,故满足(1)式的
,故满足(1)式的
最大值是63. 当n=63时,最后1个数是第 个,其值为
个,其值为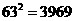 ,这是个奇数.
,这是个奇数.
据此,这一行应全为奇数.由此倒推6数,则第2010个“合格数”是3969-2×6=3957.
(三)抽丝剥茧,水落石出
[题3]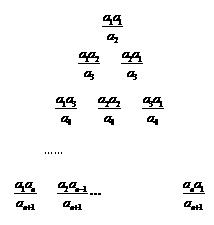 (2010四月.湖北黄冈等6市.10题)已知数列
(2010四月.湖北黄冈等6市.10题)已知数列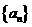 满足:
满足:
且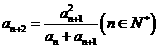 ,则图3中第5行所有数的和是( )
,则图3中第5行所有数的和是( )
A.62 B.64 C.32 D.34
[分析]求和的前提条件是找出这个递推数列的通项公式.可是由
递推关系找到求通项的规律,不是轻而易举的事,需要作逐步精密的探究.
如果不作,这道题很难.
[解析]第一步:递推关系式的右式,分子的次数高于分母的次数,
且分子为单项式,分母为多项式,不便于推理运算,因此考虑岸边取倒数.
由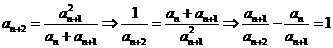
第二步,由以上结果及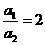 ,知
,知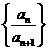 是首项
是首项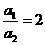 且公差d=1的等差数列.这个“过渡数列”的通项公式是:
且公差d=1的等差数列.这个“过渡数列”的通项公式是: .
.
第三步,我们发现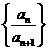 虽然不是等比数列,但其比值是一个简单的一次式.这种情况适合“叠乘法”求通项:
虽然不是等比数列,但其比值是一个简单的一次式.这种情况适合“叠乘法”求通项:
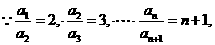
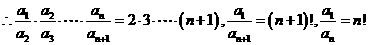
已知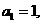 ∴这个数列的通项公式为
∴这个数列的通项公式为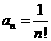 (n=1也适合)
(n=1也适合)
于是“水落石出”,图5中第5行所有数的和是:
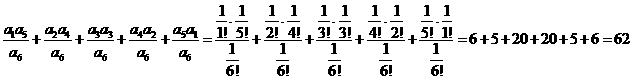
故选A.
(四)瞒天过海 暗云飞渡
 [题4](武汉二月调考.15题)已知双曲线
[题4](武汉二月调考.15题)已知双曲线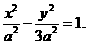 的左顶点为A,右焦点为F,设P为第一象限内曲线上的任意一点,若∠PFA=λ∠FAP,则λ的值为
的左顶点为A,右焦点为F,设P为第一象限内曲线上的任意一点,若∠PFA=λ∠FAP,则λ的值为
[分析]无论是选择题,还是填空题,都是无需讲道理的.既如此,解题人就可以省去一切繁文缛节,“不择手段”地去找出正确的答案.显然,本题的答案与非零实数a的取值范围无关,我们就可以挑选一个最便于计算的特殊位置解之.
 [解析]如图4,取图形的特殊位置,使PF⊥AF.
[解析]如图4,取图形的特殊位置,使PF⊥AF.
由条件知有A(-a,0),F(2a,0).在双曲线方程中令x=2a,有:
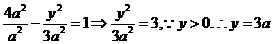 .得P(2a,3a).
.得P(2a,3a).
在直角三角形AFP中, ∴∠PAF=45°,而
∴∠PAF=45°,而
∠PFA=90°=2∠PAF.∴λ=2.
[说明](1)原题没有对点P在第一象限曲线上的位置
有所限制,这意味着λ的取值与点P的具体位置无关,也就是
λ是一个常数.这就是本题可以取特殊位值的根本原因.
(2)本题源于如下轨迹题:已知定点A(-a,0),F(2a,0).
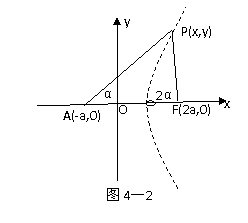 一动点p(x,y)满足∠PFA=2∠PAF,求点P的轨迹.
一动点p(x,y)满足∠PFA=2∠PAF,求点P的轨迹.
[解析]如图4--2,设∠PAF=α,则∠PFA=2α.
 .由正切的二倍角公式:
.由正切的二倍角公式:
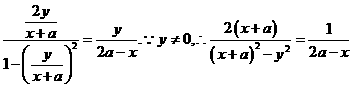

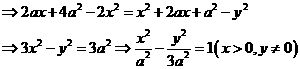
所求轨迹为双曲线的右支(不含右顶点).
(五)他山之石 可以攻玉
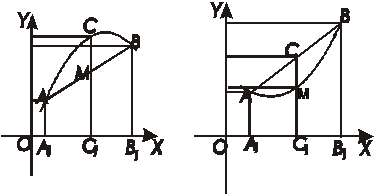
[题5](2010.武汉二月调考.10题). 过定点P(3,1)的直线 交x轴正半轴于A, 交y轴正半轴于B,O为坐标原点,则△OAB周长的最小值为(
)
交x轴正半轴于A, 交y轴正半轴于B,O为坐标原点,则△OAB周长的最小值为(
)
A.8
B.10
C.12
D.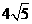
[分析1]本题是名副其实的“不小的小题”,不能用特殊值法解决,从形式上看,由于题中有坐标系为背景,是一道解析法求最值的问题.但是若真用解析几何的方法去做,却何其难也.假如思考方向不限于解析法,例如用三角法去做,却是“山穷水复疑无路,柳暗花明又一村”
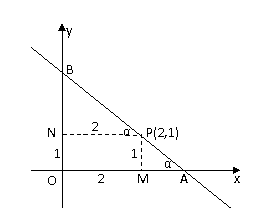 [解析1]如图1,作PM⊥x轴于M,PN⊥y轴于N,则ON=2,ON=1.
[解析1]如图1,作PM⊥x轴于M,PN⊥y轴于N,则ON=2,ON=1.
设∠OAB=∠NPB=α,则NB=2tonα,MA=cotα,AP=cscα,PB=2secα.
于是△OAB的周长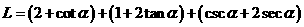
|
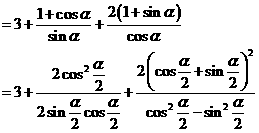
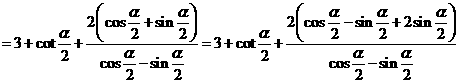
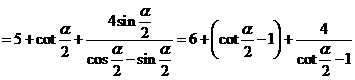
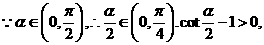 于是
于是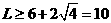 ,故选B.
,故选B.
[说明]进一步研究:当且仅当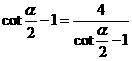 ,即
,即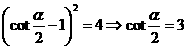 时等式成立.此时
时等式成立.此时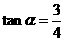 .于是
.于是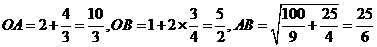 ,满足OA+AB+OB=10.
,满足OA+AB+OB=10.
[分析2]在华中师大数学通讯网站上,一位朋友利用几何思想给出了本题的绝妙解法,现介绍如下:
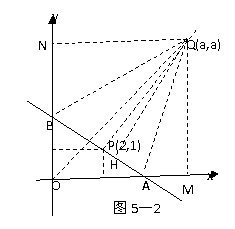 [解析2]首先证明:直角三角形的周长等于其斜边上旁切圆的直径.
[解析2]首先证明:直角三角形的周长等于其斜边上旁切圆的直径.
如图2,设直角△OAB斜边上旁切圆的圆心为Q(a,a)
作QH⊥AB于H, QM⊥x轴于M,QN⊥y轴于N那么QM=QN=QH=a.由△QAM≌△QAP知QM=QH,且AM=AH.同理QN=QH且BN=BH.于是L=QM+QN=2QH=2a.
连PQ,则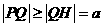 .令
.令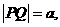 即
即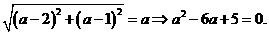
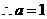 (舍),或
(舍),或 .于是所求△OAB的最小值为L=2a=10.
.于是所求△OAB的最小值为L=2a=10.
本题还可以用导数法求解,这里从略.
(六)避实击虚 反客为主
[题6](2007.北京海淀区高三数学期中试题8):已知函数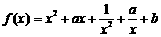
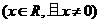
.若实数 使得
使得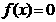 有实根,则
有实根,则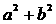 的最小值为(
的最小值为( )
)
(A)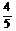
 (B)
(B)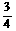
 (C)1
(C)1 (D)2
(D)2
[分析题目给定的是关于变量x的分式方程,就提论题地去做,无异于打一场耗时费力的攻坚战,希望渺茫.但若将方程中的辅助变量a,b“反客为主”,则在我们面前很快展现出一方可以自由驰骋的新天地.
[解解析]将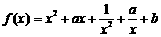 改写为:
改写为: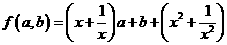 .
.
令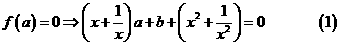
在直角坐标系aOb中,设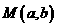 为直线(1)上一点,则
为直线(1)上一点,则 .
.
又设原点到直线(1)的距离为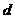 ,那么
,那么
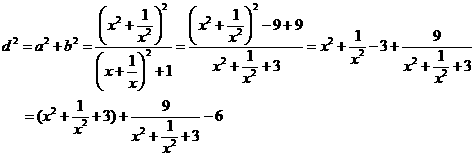
再令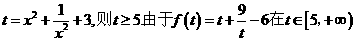 上增,故
上增,故
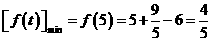 .也就是
.也就是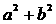 的最小值为
的最小值为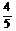 ,选(A)
,选(A)
(七)擒贼擒王 解题寻根
[题7](2005.湖北卷.6题):在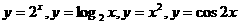 这四个函数中,
这四个函数中,
当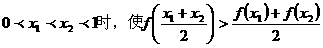 恒成立的函数的个数是( )
恒成立的函数的个数是( )
A,0 B,1 C,2 D,3
[分析]虽然是一道小题,可就是这一道不起眼的小题,那一届却难倒了一大批考生.即使是考后,有些教师为了解这道题也费了九牛二虎之力.为什么因为题中的四个函数,如果逐一探究,哪都不是省油的灯.为此人们不得不反思:擒贼擒王,解题寻根.这道题的根究竟在哪里呢?
 原来除直线函数外,无论什么函数的图像都是曲线,而曲线只有“上凸”和“下凹”两种简单形式,这就是本题的“根”.
原来除直线函数外,无论什么函数的图像都是曲线,而曲线只有“上凸”和“下凹”两种简单形式,这就是本题的“根”.
[解析]解本题应先掌握凸,凹函数的性质,
如图6-1,曲线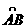 在弦AB的上方,我们
在弦AB的上方,我们
称它是上凸的函 数,在曲线上任取两点
A,B,作
 有
有
|
|
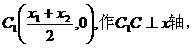 交
交 于C,AB于M,
于C,AB于M,
那么
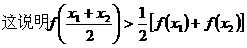
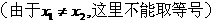 ,如图 6-2,曲线
,如图 6-2,曲线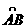 在弦AB的下方,我们称它是下凹的函 数,同理,由
在弦AB的下方,我们称它是下凹的函 数,同理,由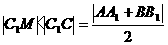 ,又说明下凹函数有性质:
,又说明下凹函数有性质: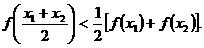
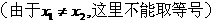
以上结论与曲线所在象限无关,这是因为曲线经过平移后,不影响它们的数量关系.
题中的四个函数,
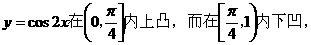 所以在(0,1)内,式子
所以在(0,1)内,式子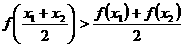 不是恒成立。又
不是恒成立。又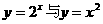 是下凹的,只有
是下凹的,只有 是上凸的,这就是说,在(0,1)内,使式子
是上凸的,这就是说,在(0,1)内,使式子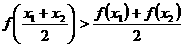
恒成立的函数只有一个。∴选B。(参看图7,1-4)
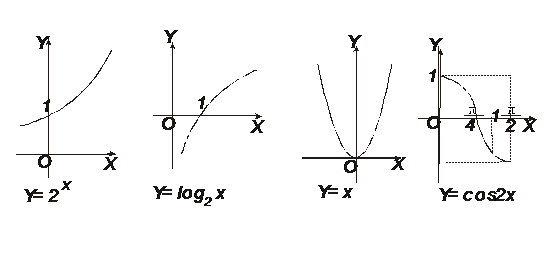
。
|
|
||||||
|
|
||||||
后记:无独有偶,今年的北京卷也有类似的试题:对于函数 ,有如下结论:①
,有如下结论:① ②
② ③
③ ④
④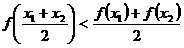
当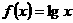 时,上述结论中正确结论的序号是本题的正确答案是②③,它与湖北卷第6题有异曲同工之妙. ,
时,上述结论中正确结论的序号是本题的正确答案是②③,它与湖北卷第6题有异曲同工之妙. ,
(八)惜墨如金 小题小作
[题8](2005.全国2卷.12题)将半径都为1的4个钢球完全装入形状为正四面体的容器里,这个正四
面体的高的最小值为( )
A 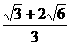 B
B
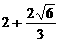 C
C
 D
D

[说明]对于这一题,笔者从某参考资料上看到的答案十分繁杂,原文如下:
[解析]正四面体的高最小时,即四个小钢球与正四面体的各个面相切。首先求出一个小球的球心O1到
另三个小球球心所在平面O2O3O4的距离(如图7--1)。
O1O2=O2O3=O3O4=O4O1=2 O2E=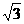 O2O=
O2O= ∴OO1=
∴OO1=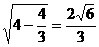
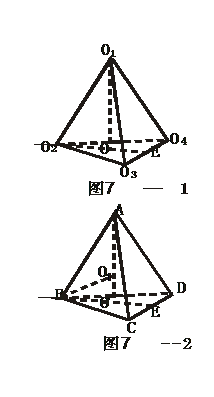 然后再求出最上面的小球的球心O1到正四面体的顶点A的距离AO1,(如图7--2)
然后再求出最上面的小球的球心O1到正四面体的顶点A的距离AO1,(如图7--2)
设AB=x 则BO,=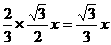 ∴O’A=
∴O’A=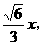 ∴O1A=
∴O1A=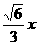 -1=O1B
-1=O1B
∵AO,⊥O,B ∴O1B2=O,O12+O,B2 ∴(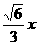 -1)2=12+
-1)2=12+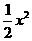
∵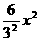 -
-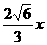 +1=1+
+1=1+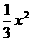 ∴
∴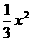 -
-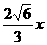 =0 ∵x≠O
∴x=
=0 ∵x≠O
∴x=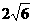
∴O,A=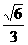 ×
×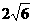 =4 ∴O1A=3
=4 ∴O1A=3
由题意可知三个球面到正四面体底面的距离为1 ,∴正四面体的高
的最小值为 3+1+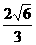 =4+
=4+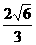
以上是正文。原文还有点评,这里从略。
就本题而言,以上的解法确实太繁了.在高考的有限时间里,花这么
大的代价是不值的.以下提出两种简略些的方法.
[解1]为求正四面体的高的最小值,只须解决三个问题:
其一,这4个钢球两两外切,其球心也连成一个正四面体,因为其棱长为2,所以它的高为2·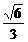 =
=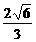 ;
;
其二,这个球心四面体与原正四面体的两底面距离为1(等于球的半径);
其三,这个球心四面体与原正四面体的两顶距离为3(等于球的半径的3倍),因此 ,这个正四面体的高
的最小值为 ,∴选C。
,∴选C。
[解2]我们不妨称原四面体为 “容器正四面体”,四个球心连成的四面体为“球心正四面体”.
“球心正四面体”与“容器正四面体”是同“中心”的相似体,相似中心就是这个共同的“中心”.
既然这个公共的中心以1∶3的比例分割了球心正四面体的高线,那么,还是这个公共的中心应以1∶3
的比例分割容器正四面体的高线.既然球心正四面体的高线向下面的底面延长了1个小球半径,那么,对应
的高线应该向上面的顶点延长3个小球半径.于是容器正四面体的高线比球心正四面体的高线共延长出4个
小球半径.因而C  是最合理的答案.
是最合理的答案.
|

|
版权所有:()
版权所有:()
1.第n行的最后1个数字是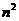 ;
;
21、(14分)一个布袋里有3个红球,2个白球,抽取3次,每次任意抽取2个,并待放回后再抽下一次,求:
(1)每次取出的2个球都是1个白球和1个红球的概率;
(2)有2次每次取出的2个球是1个白球和1个红球,还有1次取出的2个球同色的概率;
(3)有2次每次取出的2个球是1个白球和1个红球,还有1次取出的2个球是红球的概率。
20、(12分)已知A={x|1<log2x<3,x∈N},B={x||x-6|<3,x∈N}
(1)从集A及B中各取一个元素作直角坐标系中点的坐标,共可得到多少个不同的点?
(2)从A∪B中取出三个不同元素组成三位数,从左到右的数字要逐渐增大,这样的三位数共有多少个?
(3)从集A中取一个元素,从B中取三个元素,可以组成多少个无重复数字且比4000大的自然数。
19、(12分)掷三颗骰子,试求:
(1)没有一颗骰子出现1点或6点的概率;
(2)恰好有一颗骰子出现1点或6点的概率。
18、(12分)设有编号为1,2,3,4,5的五个球和编号为1,2,3,4,5的五个盒子,现将这五个球放入5个盒子内
(1)只有一个盒子空着,共有多少种投放方法?
(2)没有一个盒子空着,但球的编号与盒子编号不全相同,有多少种投放方法?
(3)每个盒子内投放一球,并且至少有两个球的编号与盒子编号是相同的,有多少种投放方法?
17、(12分)在二项式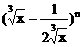 的展开式中,前三项系数的绝对值成等差数列
的展开式中,前三项系数的绝对值成等差数列
(1)求展开式的第四项;
(2)求展开式的常数项;
(3)求展开式中各项的系数和。
16、5人担任5种不同的工作,现需调整,调整后至少有2人与原来工作不同,则共有多少种不同的调整方法?________________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com