6．函数的单调性

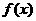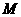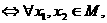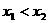⑴单调性的定义：在区间上是增(减)函数当时；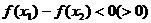

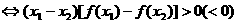
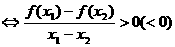⑵单调性的判定定义法：注意：一般要将式子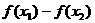化为几个因式作积或作商的形式，以利于判断符号；②导数法(见导数部分)；③复合函数法(见2 (2))；④图像法。

注：证明单调性主要用定义法和导数法。

5．函数的奇偶性⑴函数的定义域关于原点对称是函数具有奇偶性的必要条件；

⑵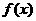是奇函数；

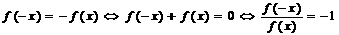⑶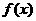是偶函数 ；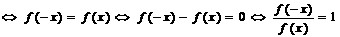

⑷奇函数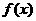在原点有定义，则；

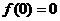⑸在关于原点对称的单调区间内：奇函数有相同的单调性，偶函数有相反的单调性；

(6)若所给函数的解析式较为复杂，应先等价变形，再判断其奇偶性；

4．分段函数：值域(最值)、单调性、图象等问题，先分段解决，再下结论。

3．复合函数的有关问题(1)复合函数定义域求法：① 若f(x)的定义域为［a，b］,则复合函数f[g(x)]的定义域由不等式a≤g(x)≤b解出② 若f[g(x)]的定义域为[a,b],求 f(x)的定义域，相当于x∈[a,b]时，求g(x)的值域。

(2)复合函数单调性的判定：①首先将原函数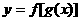分解为基本函数：内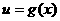函数与外函数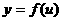；②分别研究内、外函数在各自定义域内的单调性；③根据“同性则增，异性则减”来判断原函数在其定义域内的单调性。

注意：外函数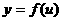的定义域是内函数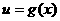的值域。

2．函数值域的求法：①直接法 ；②配方法 ；③导数法 ；④利用函数单调性 ；⑤换元法 ；

⑥利用均值不等式 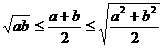； ⑦利用数形结合或几何意义(斜率、距离、绝对值的意义等)；⑧利用函数有界性(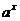、、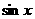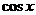等)；⑨判别式法

1．映射：注意 ①第一个集合中的元素必须有象；②一对一，或多对一。

3．(1)含n个元素的集合的子集数为2ⁿ,真子集数为2ⁿ－1；非空真子集的数为2ⁿ-2；

(2)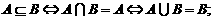 注意：讨论的时候不要遗忘了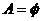的情况；

(3)。

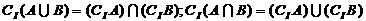2．数形结合是解集合问题的常用方法：解题时要尽可能地借助数轴、直角坐标系或韦恩图等工具，将抽象的代数问题具体化、形象化、直观化，然后利用数形结合的思想方法解决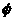；是任何集合的子集，是任何非空集合的真子集。

1．理解集合中元素的意义是解决集合问题的关键：元素是函数关系中自变量的取值？还是因变量的取值？还是曲线上的点？… ；

13．四川汶川抗震指挥部决定建造一批简易房(房型为长方体状，房高2.5米)，前后墙用2.5米高的彩色钢板，两侧用2.5米高的复合钢板，两种钢板的价格都用长度来计算(即：钢板的高均为2.5米，用钢板的长度乘以单价就是这块钢板的价格)，每米单价：彩色钢板为450元，复合钢板为200元.房顶用其它材料建造，每平方米材料费为200元.每套房材料费控制在32000元以内.

(1)设房前面墙的长为x，两侧墙的长为y，所用材料费为p，试用x,y表示p；

(2)简易房面积S的最大值是多少？并求当S最大时，前面墙的长度应设计为多少米？