8．已知P是双曲线－＝1右支上的一点，双曲线的一条渐近线方程为3x－y＝0.设F₁、F₂分别为双曲线的左、右焦点．若|PF₂|＝3，则|PF₁|＝________.

解析：∵双曲线－＝1的渐近线方程为3x－y＝0，∴a＝1，又P是双曲线的右支上一点，|PF₂|＝3，|PF₁|－|PF₂|＝2，|PF₁|＝5.

答案：5

7．已知双曲线的右焦点为(5,0)，一条渐近线方程为2x－y＝0，则双曲线的标准方程为__________．

解析：据题意由c＝5，＝2，a²+b²＝c²⇒a²＝5，b²＝20，故双曲线方程为－＝1.

答案：－＝1

6．双曲线－＝1(a>0，b>0)的两个焦点为F₁、F₂，若P为其上一点，且|PF₁|＝2|PF₂|，则双曲线离心率的取值范围为　　　　　　　　　　　　　　　　　　　　　　 (　)

A．(1,3)　 　　　　　　　　　　　B．(1,3]

C．(3，+∞) 　　　　　　　　　D．[3，+∞)

解析：∵|PF₁|－|PF₂|＝|PF₂|＝2a，而双曲线右支上到右焦点距离最近的点为右顶点，∴有c－a≤2a，∴1<e≤3，故选B.

答案：B

5．已知双曲线－＝1(a>0，b>0)的一条渐近线为y＝kx(k>0)，离心率e＝k，则双曲线方程为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.－＝1　 　　　　　　　　　B.－＝1

C.－＝1　 　　　　　　　　　D.－＝1

解析：由题意知，k＝，

∵e＝k＝·，即＝，

∴c＝b，c²＝5b²，∴a²＝c²－b²＝4b².

故选C.

答案：C

4．(2009·全国卷Ⅰ)设双曲线－＝1(a>0，b>0)的渐近线与抛物线y＝x²+1相切，则该双曲线的离心率等于　　　　　　　　　　　　　　 　　　　　　　　　　　　(　)

A. 　　　　　　　　　　　　B．2

C.　 　　　　　　　　　　　　D.

解析：双曲线的渐近线方程为y＝±x，与抛物线方程联立得x²±x+1＝0，Δ＝²－4＝0⇒b²＝4a²，

∴c²－a²＝4a²，∴c²＝5a²，e＝.故选C.

答案：C

3．设a>1，则双曲线－＝1的离心率e的取值范围是　 　　　　　(　)

A．(，2)　 　　　　　　　　B．(，)

C．(2,5)　 　　　　　　　　　　D．(2，)

解析：e＝＝　 www.k@s@5@　　　　　　　　　　　　　　 高#考#资#源#网

＝＝.

∵a>1，∴0<<1，

∴1<1+<2，

∴<e<，故选B.

答案：B

2．(2009·宁夏/海南高考)双曲线－＝1的焦点到渐近线的距离为　　　　 (　)

A．2 　　　　　　　　　　B．2

C.　 　　　　　　　　　　　D．1

解析：双曲线－＝1的焦点为(4,0)、(－4,0)．渐近线方程为y＝±x.由双曲线的对称性可知，任一焦点到任一渐近线的距离相等．d＝＝2.

答案：A

1．(2009·安徽高考)下列曲线中离心率为的是(　)

A.－＝1　 　　　　　　　　B.－＝1

C.－＝1 　　　　　　　　D.－＝1

解析：双曲线离心率e＝＝＝＝，知＝，只有B选项符合，故选B.

答案：B

⑴综合法

一般地，利用已知条件和某些数学定义、定理、公理等，经过一系列的推理论证，最后推导出所要证明的结论成立，这种证明方法叫做综合法。综合法又叫顺推法或由因导果法。

⑵分析法

一般地，从要证明的结论出发，逐步寻求使它成立的充分条件，直至最后，把要证明的结论归结为判定一个明显成立的条件(已知条件、定义、定理、公理等)，这种证明的方法叫分析法。分析法又叫逆推证法或执果索因法。

2．间接证明------反证法

一般地，假设原命题不成立，经过正确的推理，最后得出矛盾，因此说明假设错误，从而证明原命题成立，这种证明方法叫反证法。

附：

◎知识性提醒：

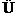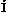1°集合与命题：设命题p，q形成的集合分别为P，Q，则p是q的充分条件PQ；

P是Q的必要条件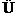P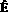Q；p是q的充要条件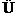P=Q。

2°角的范围：①直线倾斜角的范围[0,π)；②向量夹角的范围[0,π]

3°用定义证明的问题：①奇偶性；②单调性(也可用导数证明)；③周期性；④等差数列；⑤等比数列。

4°参数问题：

①方程、函数、不等式的最高次项系数应考虑是否为零，如对ax²+bx+c的二次项系数要注意到a>0，a=0，a<0的情况.

③　　 二次函数在某区间上的最值，可考虑对称轴的情况。

③在一元二次方程的实根分布讨论中，当方程的两根分别在两个区间内时，仅列出端点函数值符号不等式组即可；当方程的两根同在一个区间内时还须考虑△与对称轴(一般成对出现)的情况。④含参数的不等式恒成立问题，可考虑用分离变量法，或变换主元法，或数形结合法，或分类讨论法等。含参数的非基本初等函数在某区间上具有某单调性问题，可先用单调性定义，然后考虑用分离变量法。或转化为其导函数(或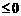)恒成立(注意检验“=”)

5°应用题：①应用题该设要设(可设出一些常量或变量)，注意量的单位及单位的统一，注意答案与实际相符。②若问题与函数、导数、不等式、数列有关。应注明定义域或注意其具有实际意义的字母的取值范围。

◎　　 易错点提醒：

1°集合是否有空集：如A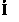B中，要注意到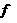A=，A≠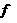；函数的定义域、值域均非空。

2°运用均值不等式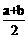≥(a,b>0)求最值时，要注意取得最值的条件“一正二定三相等”。

3°数列问题：①已知S_n，求a_n时，a_n=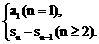(若能合并，则尽量合并成一个式子。)

②求等比数列{a_n}的前n项和S_n时，必须考虑q=1与q≠1两种情况。

③等比数列的公比和任一项都不为0，即q≠0，a_n≠0。有时对等比数列的公比分q=1，q＞1，0≠q＜1三种情况讨论。

④在等差或等比数列中，注意基本量思想(用a₁，d或q表示)，或基本性质解题(有时特别是小题)。

4°应用点斜式y=kx+b设直线方程时，应注意对斜率k是否存在要进行讨论。有时为避免讨论或方便起见，设直线方程为x=my+n，应注意此时直线不可能垂直于y轴。

◎规范化提醒

这是取得高分的基本保证。规范化包括：解题过程有必要的文字说明或叙述，注意解完后再看一下题目，看你的解答是否符合题意，谨防因解题不全或失误，答题或书写不规范而失分。总之，要吃透题“情”，合理分配时间，做到一准、二快、三规范。特别是要注意解题结果的规范化。

1°解与解集：方程的结果一般用解表示(除非强调求解集)；不等式、三角方程的结果一般用解集(集合或区间)表示，三角方程的通解中必须加k∈Z。在写区间或集合时，要正确地书写圆括号、方括号或花括号，区间的两端点之间、集合的元素之间用逗号隔开。

2°带单位的计算题或应用题，最后结果必须带单位，特别是应用题解题结束后一定要写符合题意的“答”。

3°分类讨论题，一般要写综合性结论。　 4°任何结果要最简。如=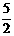,等。

5°单调区间应写成区间形式。　 　　　　6°分数线要划横线，不用斜线。

7°函数问题一般要注意定义域。

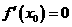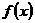8°导数是仅仅是在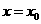处有极值的必要条件。　　 　　　　　　

[几个常用数据]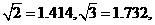　

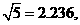
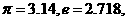
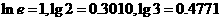； 1弧度　 ；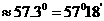

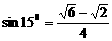
※答题要求：填空题要细做；基本题要稳做；高难题要敢做。

※解题策略：逮老鼠　　　　 吃猪肘子

◎友情提醒：将你会做的---看对了！算对了！写对了！！你就成功了！！！

周家忠编制

　　　　　　　　　　　　　　　　 2010-1-18

1．推理：

⑴合情推理：归纳推理和类比推理都是根据已有事实，经过观察、分析、比较、联想，在进行归纳、类比，然后提出猜想的推理，我们把它们称为合情推理。

①归纳推理：由某类食物的部分对象具有某些特征，推出该类事物的全部对象都具有这些特征的推理，或者有个别事实概括出一般结论的推理，称为归纳推理，简称归纳。

注：归纳推理是由部分到整体，由个别到一般的推理。

②类比推理：由两类对象具有类似和其中一类对象的某些已知特征，推出另一类对象也具有这些特征的推理，称为类比推理，简称类比。

注：类比推理是特殊到特殊的推理。

⑵演绎推理：从一般的原理出发，推出某个特殊情况下的结论，这种推理叫演绎推理。

注：演绎推理是由一般到特殊的推理。

“三段论”是演绎推理的一般模式，包括：⑴大前提---------已知的一般结论；⑵小前提---------所研究的特殊情况；⑶结　 论---------根据一般原理，对特殊情况得出的判断。