5．(2010·长望浏宁模拟)从一块短轴长为2b的椭圆形玻璃镜中划出一块面积最大的矩形，其面积的取值范围是[3b^2,4b²]，则这一椭圆离心率e的取值范围是　　　　　　　　　 (　)

A．[，]　 　　　　　　　　　　　　　 B．[，]

C．[，]　 　　　　　　　　　　　　　 D．[，]

解析：设椭圆的长轴长为2a，则矩形的最大面积为2ab，∴3b²≤2ab≤4b²，即≤≤2，又∵b＝，∴∈[，]，即∈[，]，解得：e∈[，]．

答案：A

4．(2009·江西高考)过椭圆+＝1(a>b>0)的左焦点F₁作x轴的垂线交椭圆于点P，F₂为右焦点，若∠F₁PF₂＝60°，则椭圆的离心率为　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.　 　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　 D.

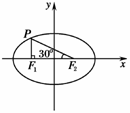
图1

解析：∵|PF₁|+|PF₂|＝2a，

又∠F₁PF₂＝60°，

∴|PF₁|＝|PF₂|，

∴|PF₂|＝2a⇒|PF₂|＝a，|PF₁|＝a，　 www.k@s@5@　　　　　　　　　　　　　　 高#考#资#源#网

在Rt△PF₁F₂中，|PF₁|²+

|F₁F₂|²＝|PF₂|²，

∴²+(2c)²＝²⇒e＝＝，故选B.

答案：B

3．若椭圆+＝1(m>n>0)上的点到右准线的距离是到右焦点距离的3倍，则m?n＝

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.　 　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　 D.

解析：由题意得该椭圆的离心率e＝＝，因此1－＝，＝，m?n＝，选D.

答案：D

2．已知椭圆+＝1，长轴在y轴上．若焦距为4，则m等于　　　　　 (　)

A．4　 　　　　　　　　　　　　　　　　　　　 B．5

C．7　 　　　　　　　　　　　　　　　　　　　 D．8

解析：因为椭圆+＝1的长轴在y轴上，所以

⇔6<m<10，又焦距为4，　 www.k@s@5@　　　　　　　　　　　　　　 高#考#资#源#网

所以m－2－10+m＝4⇔m＝8，选择D.

答案：D

1．(2009·陕西高考)“m>n>0”是“方程mx²+ny²＝1表示焦点在y轴上的椭圆”的

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．充分而不必要条件　　　　 B．必要而不充分条件

C．充要条件　 　　　　　　　　　　　　　 D．既不充分也不必要条件

解析：把椭圆方程化为+＝1.若m>n>0，则>>0.所以椭圆的焦点在y轴上．反之，若椭圆的焦点在y轴上，则>>0即有m>n>0.故选C.

答案：C

13．(20分)已知M(－2,0)，N(2,0)两点，动点P在y轴上的射影为H，且使·与·分别是公比为2的等比数列的第三、四项．

(1)求动点P的轨迹C的方程；　 www.k@s@5@　　　　　　　　　　　　　　 高#考#资#源#网

(2)已知过点N的直线l交曲线C于x轴下方两个不同的点A、B，设R为AB的中点，若过点R与定点Q(0，－2)的直线交x轴于点D(x_0,0)，求x₀的取值范围．

解：(1)M(－2,0)，N(2,0)，设动点P的坐标为(x，y)，所以H(0，y)，所以＝(－x,0)，＝(－2－x，－y)，＝

(2－x，y)，·＝x²，·＝－(4－x)²+y²由条件得y²－x²＝4，又因为是等比，所以x²≠0，所求动点的轨迹方程y²－x²＝4(x≠0)．

(2)设直线l的方程为y＝k(x－2)，A(x₁，y₁)，B(x₂，y₂)，联立方程得

∴y²－y－8＝0.

∴y₁+y₂＝，y₁·y₂＝－.

∴解得：<k<1，

R，k_RQ＝.

直线RQ的方程为y+2＝x，

∴x₀＝＝，

∴2<x₀<2+2.

图3

12．(15分)设x，y∈R，i、j为直角坐标平面内x，y轴正方向上的单位向量，若向量a＝xi+(y+2)j，b＝xi+(y－2)j，且|a|－|b|＝2.

(1)求点M(x，y)的轨迹C的方程；

(2)已知直线l过点A(，0)，斜率为k(0<k<1)时，若轨迹C上有且仅有一点B到直线l的距离为，试求k的值．

解：(1)由|a|－|b|＝2以及a＝xi+(y+2)j，b＝xi+(y－2)j知M(x，y)到点(0，－2)和(0,2)的距离之差为常数2，所以，M(x，y)的轨迹为以(0，－2)和(0,2)为焦点，实轴长为2的双曲线的上支，其方程为－＝1(y>0)．

(2)显然，直线l的方程为y＝k(x－)，与直线l平行且距离为的直线为l′：y＝kx+d，则由＝可求得d＝－k.所以，l′的方程为y＝kx+－k.

由于l′与C的渐近线不平行，因此，根据题设可知，直线l′与双曲线C相切．将直线l′的方程代入双曲线C的方程－＝1，有(kx+－k)²－x²＝2，即

(k²－1)x²+2(－k)kx+(－k)²－2＝0.

由

可以解得k＝.

图2

11．(15分)已知双曲线的方程是16x²－9y²＝144.

(1)求这双曲线的焦点坐标、离心率和渐近线方程；

(2)设F₁和F₂是双曲线的左、右焦点，点P在双曲线上，且

|PF₁|·|PF₂|＝32，求∠F₁PF₂的大小．

解：(1)由16x²－9y²＝144得－＝1，

∴a＝3，b＝4，c＝5.

焦点坐标F₁(－5,0)，F₂(5,0)，离心率e＝，渐近线方程为y＝±x.

(2)||PF₁|－|PF₂||＝6，

cos∠F₁PF₂＝

＝

＝＝0.

∴∠F₁PF₂＝90°.

10．(2009·东北三校)已知双曲线－＝1(a>0，b>0)的离心率的取值范围是e∈[，2]，则两渐近线夹角的取值范围是__________．

解析：e²∈[，4]，∴≤≤4，∴≤≤，设夹角为α，可得≤≤，∵α≤，∴≤α≤.

答案：[，]　 www.k@s@5@　　　　　　　　　　　　　　 高#考#资#源#网

9．(2009·湖南高考)已知以双曲线C的两个焦点及虚轴的两个端点为顶点的四边形中，有一个内角为60°，则双曲线C的离心率为________．

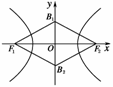
图1

解析：如图1，∵c>b，∴∠B₁F₁B₂＝60°，∠B₁F₁O＝30°，在△B₁OF₁中，＝tan30°，∴＝，∴＝，∴1－＝⇒＝，∴e²＝＝，∴e＝.

答案：