2．直线x－y+m＝0与圆x²+y²－2x－2＝0相切，则实数m等于　　　　　　　　　 (　)

A.或－　 　　　　　　　　　　　　　 B．－或3

C．－3或　 　　　　　　　　　　　 D．－3或3

解析：把圆的方程化成标准方程(x－1)²+y²＝3，

由已知得＝，

即|m+|＝2，

∴m＝－3或m＝.故选C.

答案：C

1．(2009·重庆高考)直线y＝x+1与圆x²+y²＝1的位置关系是　　　　　　　　　　　　 (　)

A．相切　 　　　　　　　　　　　　　　　　 B．相交但直线不过圆心

C．直线过圆心　 　　　　　　　　　　　 D．相离

解析：圆心(0,0)到直线y＝x+1的距离为d＝＝，圆的半径r＝1，∴0<d<r.

∴直线与圆相交但不过圆心．

答案：B

13．(20分)(2009·四川高考)已知椭圆+＝1(a>b>0)的左、右焦点分别为F₁、F₂，离心率e＝，右准线方程为x＝2.

(1)求椭圆的标准方程；

(2)过点F₁的直线l与该椭圆相交于M、N两点，且|+|＝，求直线l的方程．

解析：(1)由条件有解得a＝，c＝1.

∴b＝＝1.

所以，所求椭圆的方程为+y²＝1.

(2)由(1)知F₁(－1,0)、F₂(1,0)．

若直线l的斜率不存在，则直线l的方程为x＝－1，

将x＝－1代入椭圆方程得y＝±.　 www.k@s@5@　　　　　　　　　　　　　　 高#考#资#源#网

不妨设M、N，

∴+＝+＝(－4,0)．

∴|+|＝4，与题设矛盾．

∴直线l的斜率存在．

设直线l的斜率为k，则直线l的方程为y＝k(x+1)．

设M(x₁，y₁)、N(x₂，y₂)，联立

消y得(1+2k²)x²+4k²x+2k²－2＝0.

由根与系数的关系知x₁+x₂＝，从而y₁+y₂＝k(x₁+x₂+2)＝.

又∵＝(x₁－1，y₁)，＝(x₂－1，y₂)，

∴+＝(x₁+x₂－2，y₁+y₂)．

∴|+|²＝(x₁+x₂－2)²+(y₁+y₂)²

＝²+²＝.

∴＝².

化简得40k⁴－23k²－17＝0，

解得k²＝1或k²＝－(舍)．∴k＝±1.

∴所求直线l的方程为y＝x+1或y＝－x－1.

12．(15分)如图4，两束光线从点

M(－4,1)分别射向直线y＝－2上两点P(x₁，y₁)和Q(x₂，y₂)后，反射光线恰好通过椭圆C：+＝1(a>b>0)的两焦点，已知椭圆的离心率为，且x₂－x₁＝，求椭圆C的方程．

解：设a＝2k，c＝k，k≠0，则b＝k，

其椭圆的方程为+＝1.

由题设条件得＝－，①

＝－，②

x₂－x₁＝，③

由①②③解得k＝1，x₁＝－，x₂＝－1，

所求椭圆C的方程为+＝1.

11．(15分)已知A(－2,0)，B(2,0)，过点A作直线l交以A、B为焦点的椭圆于M、N两点，线段MN的中点到y轴的距离为，且直线l与圆x²+y²＝1相切，求该椭圆的方程．

解：易知直线l与x轴不垂直，设直线l的方程为y＝k(x+2)．①

又设椭圆方程为+＝1(a²>4)．　　　　　　　　　　　 ②

因为直线l与圆x²+y²＝1相切，故＝1，

解得k²＝.将①代入②整理得，

(a²k²+a²－4)x²+4a²k²x+4a²k²－a⁴+4a²＝0，而k²＝，即(a²－3)x²+a²x－a⁴+4a²＝0，

设M(x₁，y₁)，N(x₂，y₂)，则x₁+x₂＝－，

由题意有＝2×(a²>3)，求得a²＝8.经检验，此时Δ>0.

故所求的椭圆方程为+＝1.

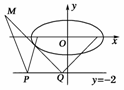
图4

10．(2010·武汉调研)如图3，已知A、B两点分别是椭圆C：+＝1(a>b>0)的左顶点和上顶点，而F是椭圆C的右焦点，若·＝0，则椭圆C的离心率e＝________.

解析：A(－a,0)，B(0，b)，F(c,0)，

∴＝(a，b)，＝(c，－b)

∴ac＝b²，即ac＝a²－c²，∴e＝1－e²，解得e＝.

答案：

9．已知A、B为椭圆C：+＝1的长轴的两个端点，P是椭圆C上的动点，且∠APB的最大值是，则实数m的值是__________．

解析：由椭圆知识知，当点P位于短轴的端点时∠APB取得最大值，根据题意则有tan＝⇒m＝.

答案：

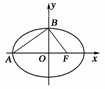
图3

8．(2009·广东高考)已知椭圆G的中心在坐标原点，长轴在x轴上，离心率为，且G上一点到G的两个焦点的距离之和为12，则椭圆G的方程为________．

解析：由题意得2a＝12，＝，所以a＝6，c＝3，b＝3.故椭圆方程为+＝1.

答案：+＝1

7．(2009·北京高考)椭圆+＝1的焦点为F₁、F₂，点P在椭圆上．若|PF₁|＝4，则|PF₂|＝__________；∠F₁PF₂的大小为__________．

解析：依题知a＝3，b＝，c＝.由椭圆定义得|PF₁|+

|PF₂|＝6，∵|PF₁|＝4，∴|PF₂|＝2.又|F₁F₂|＝2.在△F₁PF₂中由余弦定理可得cos∠F₁PF₂＝－，∴∠F₁PF₂＝120°

答案：2　120°

6．(2009·全国卷Ⅰ)已知椭圆C：+y²＝1的右焦点为F，右准线为l，点A∈l，线段AF交C于点B.若＝3，则||＝　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

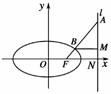
图2

A.　　　　　　　　　　　　　　　　　 B．2

C.　　　　　　　　　　　　　　　　　 D．3

解析：如图2，BM垂直于右准线于M，右准线与x轴交于N，易求得椭圆的离心率为e＝，由椭圆的第二定义得BM＝，在Rt△AMB中，＝＝＝，它为等腰直角三角形，则△ANF也为等腰直角三角形，FN＝＝1，则||

＝.故选A.

答案：A