3．(2009·陕西高考)若x，y满足约束条件目标函数z＝ax+2y仅在点(1,0)处取得最小值，则a的取值范围是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

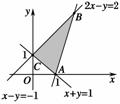
图3

A．(－1,2)　　　　　　　　　　 B．(－4,2)

C．(－4,0]　 　　　　　　　　　　　 D．(－2,4)

解析：可行域为△ABC，如图3

当a＝0时，显然成立．当a>0时，直线ax+2y－z＝0的斜率k＝－>k_AC＝－1，a<2.

当a<0时，k＝－<k_AB＝2，∴a>－4.

综合得－4<a<2，故选B.

答案：B

2．(2009·天津高考)设变量x、y满足约束条件则目标函数z＝2x+3y的最小值为　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．6　 　　　　　　　　　　　　　　　 B．7

C．8　 　　　　　　　　　　　　　　　 D．23

解析：约束条件表示的平面区域如图2　　

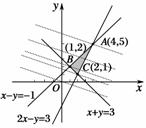
图2

易知过C(2,1)时，目标函数z＝2x+3y取得最小值．

∴z_min＝2×2+3×1＝7.故选B.

答案：B

1．若实数x、y满足则的取值范围是　　　　　　　　　　　　　　　　　　　 (　)

A．(0,1)　　　　 B．(0,1]

C．(1，+∞)　 　　　　　　　　　 D．[1，+∞)

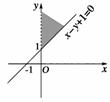
图1

解析：先作出可行域如图1，而＝，可作为点(x，y)与原点连线的斜率，故选C.

答案：C

13．(20分)两条互相平行的直线分别过点A(6,2)和B(－3，－1)，并且各自绕着A、B旋转，如果两条平行直线间的距离为d，求：

(1)d的变化范围；

(2)当d取最大值时，两条直线的方程．

解：(1)方法1：①当两条直线的斜率不存在时，即两直线分别为x＝6和x＝－3，则它们之间的距离为9.

②当两条直线的斜率存在时，设这两条直线方程为

l₁：y－2＝k(x－6)，

l₂：y+1＝k(x+3)，

即l₁：kx－y－6k+2＝0，l₂：kx－y+3k－1＝0.

∴d＝＝，

即(81－d²)k²－54k+9－d²＝0.

∵k∈R，且d≠9，d>0，

∴Δ＝54²－4(81－d²)(9－d²)≥0，

即0<d≤3且d≠9.

综合①②可知，所求的d的变化范围为(0,3]．

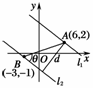
图4

方法2：如图4所示，

显然有0<d≤|AB|.

而|AB|＝

＝3.

故所求的d的变化范围为(0,3]．

(2)由图4可知，当d取最大值时，两直线垂直于AB.

而k_AB＝＝，

∴所求的直线的斜率为－3.

故所求的直线方程分别为y－2＝－3(x－6)和y+1＝

－3(x+3)，即3x+y－20＝0和3x+y+10＝0.

12．(15分)△ABC中，A(1,4)，∠ABC的平分线所在直线方程为x－2y＝0，∠ACB的平分线所在直线的方程为x+y－1＝0(如图3)，求BC边所在直线的方程．

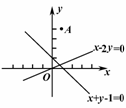
图3

解：设A点关于直线x－2y＝0的对称点为A₁(x₁，y₁)，则有

，可解得即A₁(，－)，

设点A关于x+y－1＝0的对称点为A₂(x₂，y₂)，

则有

解得.即A₂(－3,0)．

则直线A₁A₂即直线BC的方程为

y＝[x－(－3)]

即4x+17y+12＝0.

11．(15分)等腰Rt△ABC的斜边AB所在的直线方程是3x－y+2＝0，C(，)，求直线AC和直线BC的方程和△ABC的面积．

解：k_AB＝3，设与直线AB夹角为45°的直线斜率为k，则＝tan45°＝1.

∴k＝或－2.∴直线AC、BC的方程为

y－＝(x－)和y－＝－2(x－)，

即x－2y－2＝0和2x+y－6＝0，

又C到直线AB的距离d＝，

∴S_△ABC＝|AB|·d＝×2×＝10. 　　

10．(2009·全国卷Ⅰ)若直线m被两平行线l₁：x－y+1＝0与l₂：x－y+3＝0所截得的线段的长为2，则m的倾斜角可以是①15°　②30°　③45°　④60°　⑤75°

其中正确答案的序号是________．(写出所有正确答案的序号)

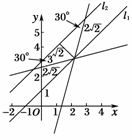
图2

解析：两平行线间的距离为d＝＝，如图2所示，可知直线m与l₁、l₂的夹角为30°，l₁、l₂的倾斜角为45°，所以直线m的倾斜角等于30°+45°＝75°或45°－30°＝15°.故填①⑤.

答案：①⑤

9．直线l₁：a₁x+b₁y+1＝0和直线l₂：a₂x+b₂y+1＝0的交点为(2,3)，则过两点Q₁(a₁，b₁)，Q₂(a₂，b₂)的直线方程为__________．

解析：∵(2,3)为两直线l₁，l₂的交点，

∴2a₁+3b₁+1＝0,2a₂+3b₂+1＝0，由此可知，

点Q₁(a₁，b₁)，Q₂(a₂，b₂)都在直线2x+3y+1＝0上，

又∵l₁与l₂是两条不同的直线，

∴a₁与a₂，b₁与b₂不可能全相同，

因此Q₁，Q₂为不同的两点，

∴过两点Q₁，Q₂的直线方程为2x+3y+1＝0.

答案：2x+3y+1＝0

8．点P(4cosθ，3sinθ)到直线x+y－6＝0的距离的最小值等于__________．

解析：由点到直线的距离公式可得

d＝＝

∵－5≤5sin(θ+φ)≤5，

∴－11≤5sin(θ+φ)－6≤－1.∴d_min＝.

答案：

7．与直线3x+4y+12＝0平行，且与坐标轴构成的三角形面积是24的直线l的方程是__________．

解析：由题意可设直线l：3x+4y+c＝0，令x＝0，y＝－，令y＝0，x＝－，∴··＝24⇒c＝±24，

∴直线l：3x+4y±24＝0.

答案：3x+4y±24＝0