13．(20分)(2009·全国卷Ⅰ)设函数f(x)＝x³+3bx²+3cx有两个极值点x₁、x₂，且x₁∈[－1,0]，x₂∈[1,2]．

(1)求b、c满足的约束条件，并在下面的坐标平面内，画出满足这些条件的点(b，c)的区域；

图10

(2)证明：－10≤f(x₂)≤－.

解：(1)f′(x)＝3x²+6bx+3c，依题意知，方程f′(x)＝0有两个根x₁、x₂，且x₁∈[－1,0]，x₂∈[1,2]等价于f′(－1)≥0，f′(0)≤0，f′(1)≤0，f′(2)≥0.

由此得b、c满足的约束条件为

满足这些条件的点(b，c)的区域为图11中阴影部分．

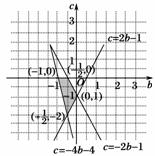
图11

(2)由题设知f′(x₂)＝3x+6bx₂+3c＝0，故bx₂＝－x－c，于是f(x₂)＝x+3bx+3cx₂＝－x+x₂.

由于x₂∈[1,2]，而由(1)知c≤0，

故－4+3c≤f(x₂)≤－+c.

又由(1)知－2≤c≤0，所以－10≤f(x₂)≤－.

12．(15分)某厂拟生产甲、乙两种试销产品，每件销售收入分别为3千元、2千元．甲、乙产品都需要在A、B两种设备上加工，在每台A、B上加工一件甲所需工时分别为1工时、2工时，加工一件乙所需工时分别为2工时、1工时，A、B两种设备每月有效使用台时数为a(400≤a≤500)．求生产收入最大值的范围．

解：设甲、乙两种产品月产量分别为x、y件，约束条件是目标函数是z＝3x+2y，

由约束条件画出可行域，如图9.

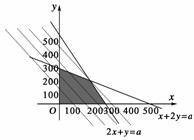
图9

将z＝3x+2y变形为y＝－x+，

这是斜率为－，随z变化的一簇直线．

是直线在y轴上的截距，当最大时z最大，当然直线要与可行域相交，即在满足约束条件时目标函数取得最大值．

由解得

在这个问题中，使z＝3x+2y取得最大值的(x，y)是两直线2x+y＝a与x+2y＝a的交点(，)．

∴z＝3·+2·＝a.

又∵400≤a≤500，∴≤z≤.

故月生产收入最大值的范围是[，]．

11．(15分)求不等式|x|+|y|≤2表示的平面区域的面积．

解：|x|+|y|≤2可化为：

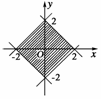
图8

或

或或

其平面区域如图8所示．

∴面积S＝×4×4＝8.

10．若A为不等式组表示的平面区域，则当a从－2连续变化到1时，动直线x+y＝a扫过A中的那部分区域的面积为__________．

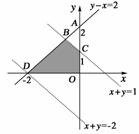
图7

解析：根据题意作图如图7：

图中阴影部分为所求的区域，设其面积为S，S＝S_△AOD－S_△ABC＝·2·2－·1·＝.

答案：

9．若a≥0，b≥0，且当时，恒有ax+by≤1，则以a、b为坐标的点P(a，b)所形成的平面区域的面积等于__________．

解析：令z＝ax+by，

∵ax+by≤1恒成立，　 　

即函数z＝ax+by在可行域要求的条件下，z_max＝1恒成立．

当直线ax+by－z＝0过点(1,0)或点(0,1)时，0≤a≤1,0≤b≤1.点P(a，b)形成的图形是边长为1的正方形．

∴所求的面积S＝1²＝1.

答案：1

8．(2009·浙江高考)若实数x、y满足不等式组则2x+3y的最小值是________．

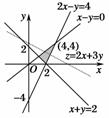
图6

解析：依题意作出可行性区域如图6，目标函数z＝2x+3y在边界点(2,0)处取到最小值z＝2×2+3×0＝4.

答案：4

7．已知点P(x₁，y₁)不在直线l：Ax+By+C＝0(B≠0)上，则P在直线l上方的充要条件是__________，P在直线l下方的充要条件是__________．

解析：直线l：Ax+By+C＝0(B≠0)上点M，其横坐标x＝x₁时，纵坐标y＝－，点P在直线l的上方等价于点P在点M的上方，即y₁>－，∴>0，亦即B(Ax₁+By₁+C)>0.所以P在直线l上方的充要条件是B(Ax₁+By₁+C)>0，同理P在直线l下方的充要条件是B(Ax₁+By₁+C)<0.

答案：B(Ax₁+By₁+C)>0　B(Ax₁+By₁+C)<0

6．(2009·湖北高考)在“家电下乡”活动中，某厂要将100台洗衣机运往邻近的乡镇，现有4辆甲型货车和8辆乙型货车可供使用．每辆甲型货车运输费用400元，可装洗衣机20台；每辆乙型货车运输费用300元，可装洗衣机10台．若每辆车至多只运一次，则该厂所花的最少运输费用为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．2000元　 　　　　　　　　　　　　　　 B．2200元

C．2400元　 　　　　　　　　　　　 D．2800元

解析：设需使用甲型货车x辆，乙型货车y辆，运输费用z元，根据题意得线性约束条件求线性目标函数z＝400x+300y的最小值．

解得当时，z_min＝2200，故选B.

答案：B

5．(2009·山东高考)设x，y满足约束条件若目标函数z＝ax+by(a＞0，b＞0)的最大值为12，则+的最小值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.　 　　　　　　　　　　　　 　　　 B. 　　

C.　 　　　　　　　　　　　　　　　　 D．4

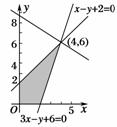
图5

解析：作可行域如图5可知，目标函数在(4,6)处取得最大值12，

∴2a+3b＝6，从而有+

＝(2a+3b)

＝

＝+

＝+≥+2＝.故选A.

答案：A

4．(2009·安徽高考)若不等式组 所表示的平面区域被直线y＝kx+分为面积相等的两部分，则k的值是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　 D.

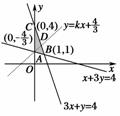
图4

解析：由图4可知，线性规划区域为△ABC边界及内部，y＝kx+恰过A，y＝kx+将区域平均分成面积相等两部分，故过BC的中点D，＝k×+，k＝，故选A.

答案：A