1．已知点P为线段AB上的一点，且P分的比为2，则点B分有向线段的比为(　)

A．－2　　　　　　 B．－3

C.　 　　　　　　　　　　　　　　　　　　　　 D．－

答案：B

13．(20分)(2009·福建高考)如图1，某市拟在长为8 km的道路OP的一侧修建一条运动赛道．赛道的前一部分为曲线段OSM，该曲线段为函数y＝Asinωx(A>0，ω>0)，x∈[0,4]的图象，且图象的最高点为S(3,2)；赛道的后一部分为折线段MNP.为保证参赛运动员的安全，限定∠MNP＝120°.

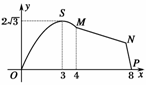
图1

(1)求A，ω的值和M，P两点间的距离；

(2)应如何设计，才能使折线段赛道MNP最长？

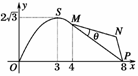
图2

解：解法1：(1)依题意，有A＝2，＝3，

又T＝，∴ω＝.

∴y＝2sinx.

当x＝4时，y＝2sin＝3，

∴M(4,3)．又P(8,0)，

∴MP＝＝5.

(2)在△MNP中，∠MNP＝120°，MP＝5.

设∠PMN＝θ，则0°<θ<60°.

由正弦定理得＝＝，　　 www.k@s@5@　　　　　　　　　　　　　　 高#考#资#源#网

∴NP＝sinθ，MN＝sin(60°－θ)．

故NP+MN＝sinθ+sin(60°－θ)

＝(sinθ+cosθ)＝sin(θ+60°)．

∵0°<θ<60°，∴当θ＝30°时，折线段赛道MNP最长．

亦即，将∠PMN设计为30°时，折线段赛道MNP最长．

解法2：(1)同解法1.

(2)在△MNP中，∠MNP＝120°，MP＝5，

由余弦定理得

MN²+NP²－2MN·NP·cos∠MNP＝MP²，

即MN²+NP²+MN·NP＝25.

故(MN+NP)²－25＝MN·NP≤()²，

从而(MN+NP)²≤25，即MN+NP≤，

当且仅当MN＝NP时等号成立．

亦即，设计为MN＝NP时，折线段赛道MNP最长．

注：本题第(2)问答案及其呈现方式均不唯一．除了解法1、解法2给出的两种设计方式，还可以设计为：①N(，)；②N(，)；③点N在线段MP的垂直平分线上等．

12．(15分)(2009·天津高考)在△ABC中，BC＝，AC＝3，sinC＝2sinA.

(1)求AB的值；

(2)求sin(2A－)的值．

解：(1)在△ABC中，根据正弦定理，＝.

于是AB＝BC＝2BC＝2.

(2)在△ABC中，根据余弦定理，

得cosA＝＝.

于是sinA＝＝.

从而sin2A＝2sinAcosA＝，cos2A＝cos²A－sin²A＝.

所以sin(2A－)＝sin2Acos－cos2Asin＝.

11．(15分)在△ABC中，cosA＝－，cosB＝.

(1)求sinC的值；

(2)设BC＝5，求△ABC的面积．

解：(1)由cosA＝－，得sinA＝，

由cosB＝，得sinB＝.

所以sinC＝sin(A+B)＝sinAcosB+cosAsinB＝.

(2)由正弦定理得

AC＝＝＝.　　 www.k@s@5@　　　　　　　　　　　　　　 高#考#资#源#网

所以△ABC的面积

S＝×BC×AC×sinC＝×5××＝.

10．在△ABC中，若＝＝，则tanA∶tanB∶tanC＝__________，tanA＝________.

解析：由＝＝，

得＝＝，∴＝＝，

结合正弦定理有：＝＝，

∴3tanB＝2tanC＝tanA，

∴tanA∶tanB∶tanC＝1∶∶＝6∶2∶3，且∠A、∠B、∠C皆为锐角．

又∵tanA＝－tan(B+C)＝－

＝，

∴tan²A－1＝，tan²A＝11，∴tanA＝.

答案：6?2?3　

9．在△ABC中，角A、B、C所对的边分别为a、b、c.若(b－c)cosA＝acosC，则cosA＝________.

解析：由正弦定理得：(sinB－sinC)cosA＝sinA·cosC⇒sinBcosA－sinCcosA＝sinA·cosC⇒sinBcosA＝sin(A+C)＝sinB.即cosA＝.

答案：

8．在△ABC中，已知BC＝12，A＝60°，B＝45°，则AC＝__________.

解析：由正弦定理得＝，即＝，

∴AC＝×＝4.

答案：4

7．已知△ABC的三个内角A、B、C成等差数列，且AB＝1，BC＝4，则边BC上的中线AD的长为__________．

解析：∵A、B、C成等差数列，∴2B＝A+C.

∵A+B+C＝π，∴B＝.

在△ABD中，AD＝

＝＝.

答案：

6．(2009·泉州质检)在锐角△ABC中，角A、B、C所对的边分别是a、b、c，设B＝2A，则b?a的取值范围是

(　)

A．(1,2)　 　　　　　　　　　　　　　　　　 B．(0,2)

C．(，2)　 　　　　　　　　　　　　　　 D．(，)

解析：＝＝2cosA，

由，得：<A<

∴cosA∈(，)，∴∈(，)．　　 www.k@s@5@　　　　　　　　　　　　　　 高#考#资#源#网

答案：D

5．已知△ABC，若对任意m∈R，|－m|≥||恒成立，则△ABC必定为

(　)

A．锐角三角形　 　　　　　　　　　　　 B．钝角三角形

C．直角三角形　 　　　　　　　　　　　 D．不确定

解析：设m＝，则由题意得||≥||，由m的任意性可知，点D可视为是直线AB上的任意一点，即对于直线AB上的任意一点D与点C的距离都不小于A、C两点间的距离，因此AC⊥AB，选C.

答案：C