11．(15分)已知A(2,3)，B(－1,5)，且满足＝，＝3，＝－，求C，D，E的坐标．

解：解法1：设C(x_C，y_C)，D(x_D，y_D)，E(x_E，y_E)．

∴＝(x_C－2，y_C－3)，＝(－3,2)．

＝(x_D－2，y_D－3)，＝(x_E－2，y_E－3)．

由条件得(x_C－2，y_C－3)＝(－3,2)，

(x_D－2，y_D－3)＝3(－3,2)，

(x_E－2，y_E－3)＝－(－3,2)．从而有

，，.

∴C(1，)，D(－7,9)，E(，)．

解法2：由＝3＝3(+)得＝－.

由＝－(+)，得＝－.

由＝＝(+)，得＝.

由定比分点公式，可得

x_C＝＝1，y_C＝＝；

x_D＝＝－7，

y_D＝＝9；

x_E＝＝，

y_E＝＝.

∴C(1，)，D(－7,9)，E(，)．

10．(2009·福建质检)P为△ABC所在平面上的点，且满足＝+，则△ABP与△ABC的面积之比是________．

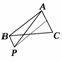
图3

解析：∵＝+，∴＝

∴P点位置如图3所示：∴＝

答案：1?2　 www.k@s@5@　　　　　　　　　　　 　　　高#考#资#源#网

9．(2009·北京西城模拟)已知点A(0,0)，B(，0)，C(0,1)．设AD⊥BC于D，那么有＝λ，其中λ＝________.

解析：如图2，|AB|＝，|AC|＝1，|CB|＝2，由于AD⊥BC，且＝λ，所以C、D、B 共线，所以＝，即λ＝.

图2

答案：

8．已知A(1,0)，B(0，－1)，P(x，y)，O为坐标原点，若＝，则P点的轨迹方程为__________．

解析：消去参数得：y＝x－1，(x≠0)．

答案：y＝x－1，(x≠0)

7．把函数y＝3^x的图象按a＝(2，－2)平移得到F′，F′的解析式为__________．

答案：y＝3^x－2－2

6．(2010·湖北八校联考)将函数f(x)＝x³+3x²+3x的图象按向量a平移后得到函数g(x)的图象，若函数g(x)满足g(x)+g(2－x)＝1，则向量a的坐标是

(　)

A．(－1，－1)　 　　　　　　　　　　　 B．(2，)

C．(2,2)　 　　　　　　　　　　　　　　　　 D．(－2，－)

解析：设平移向量a＝(m，n)，(x，y)是函数f(x)＝x³+3x²+3x图象上任意点的坐标，(x′，y′)是按向量a＝(m，n)平移后函数g(x)图象上对应点的坐标，则平移公式，代入f(x)＝x³+3x²+3x得g(x′)＝(x′－m+1)³－1+n，由于g(x)+g(2－x)＝1，(1－m+x)³－1+n+(3－m－x)³－1+n＝1，整理并解得m＝2，n＝，选择B.

答案：B

5．将函数y＝sinωx(ω>0)的图象按向量a＝(－，0)平移，平移后的图象如图1所示，则平移后的图象所对应函数的解析式是

(　)

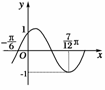
图1

A．y＝sin(x+)

B．y＝sin(x－)

C．y＝sin(2x+)

D．y＝sin(2x－)

解析：由图象可看出ω＝＝＝2.

按向量a＝(－，0)平移，即向左平移个单位．

平移后的函数解析式为y＝sin[2(x+)]＝sin(2x+)．

答案：C

4．(2010·河北实验中学检测)若已知函数y＝的图象按向量n＝(b,0)平移后得到函数y＝的图象，则函数f(x)＝a^x－b(a>0且a≠1)的反函数的图象恒过定点

(　)

A．(2,1)　 　　　　　　　　　　　　　　　　 B．(1,2)

C．(－2,1)　 　　　　　　　　　　　　　　 D．(0,2)

解析：函数y＝的图象按n＝(b,0)平移后得到函数y＝的图象，∴b＝2.

f(x)＝a^x－2恒过(2,1)点，f^－1(x)恒过(1,2)点．

答案：B

3．已知点A(2,3)，B(10,5)，直线AB上一点P满足||＝2||，则点P的坐标是(　)

A．(，)　 　　　　　　　　　　　　　 B．(18,7)

C．(，)或(18,7)　 　　　　　　　 D．(18,7)或(－6，－1)

解析：设＝λ，由||＝2||可知λ＝±2，由定比分点坐标公式可得P点坐标为(，)或(18,7)．

答案：C　 www.k@s@5@　　　　　　　　　　　　　　 高#考#资#源#网

2．已知△ABC的三个顶点分别是A(1，)，B(4，－2)，

C(1，y)，重心为G(x，－1)，则x、y的值分别是

(　)

A．x＝2，y＝5　 　　　　　　　　　　　 B．x＝1，y＝－

C．x＝1，y＝－1　 　　　　　　　　　 D．x＝2，y＝－

解析：由重心坐标公式x＝＝2，－1＝⇒y＝－.

答案：D