
题目列表(包括答案和解析)
(11) 不等式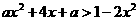 对一切
对一切 R恒成立,则实数a的取值范围是_______.
R恒成立,则实数a的取值范围是_______.
(12)函数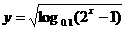 的定义域是_____________.
的定义域是_____________.
(13)不等式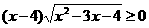 的解集是____________.
的解集是____________.
(14) 若关于x的不等式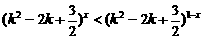 的解集是
的解集是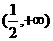 ,则实数k的取值范围是____________.
,则实数k的取值范围是____________.
(1) 下列不等式中与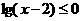 同解的是
(
)
同解的是
(
)
(A) (B)
(B)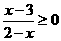
(C)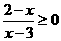 (D)
(D)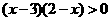
(2) 不等式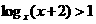 的解集是
(
)
的解集是
(
)
(A)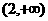 (B)
(B)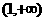
(C)(0,1)
(D)(0,1)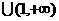
(3) 不等式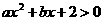 的解集是
的解集是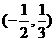 ,则a+b的值是
(
)
,则a+b的值是
(
)
(A)10 (B)-10 (C)14 (D)-14
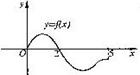
(4) 设奇函数f(x)的定义域为[-5,5].若当x∈[0,5]时, f(x)的图象如右图,则不等式f(x)<0的
解是 ( )
 (A) (-5,-2)∪(2,
(A) (-5,-2)∪(2,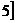
(B) (-5,-2)∪(2,5)
(C) [-2,0]∪(2,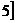
(D) (-2,0)∪(2,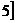
(5) 不等式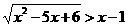 的解集是
(
)
的解集是
(
)
(A)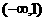 (B)
(B) 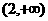 (C)
(C)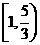 (D)
(D)
(6) 已知集合M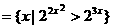 ,N
,N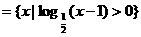 则M
则M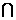 N=
(
)
N=
(
)
(A)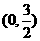 (B)
(B)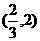 (C)
(C)
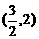 (D)(0,1)
(D)(0,1)
(7) 在R上定义运算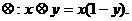 若不等式
若不等式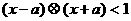 对任意实数
对任意实数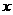 成
成
立,则 ( )
(A)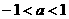 (B)
(B)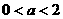 (C)
(C)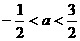 (D)
(D)
(8) 若不等式x2-2ax+a>0,对 x∈R恒成立, 则关于t的不等式 <1的解为 ( )
<1的解为 ( )
(A) 1<t<2 (B) -2<t<1 (C)-2<t<2 (D) -3<t<2
(9) 设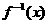 是函数
是函数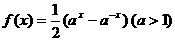 的反函数,则使
的反函数,则使 成立的x的
成立的x的
取值范围为 ( )
(A)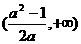 (B)
(B)
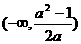 (C)
(C) 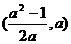 (D)
(D) 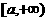
(10) 设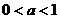 ,函数
,函数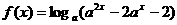 ,则使
,则使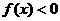 的
的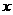 的取值范围是( )
的取值范围是( )
(A)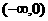 (B)
(B)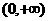 (C)
(C)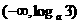 (D)
(D)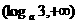
13.(20分)(2009·江西高考)各项均为正数的数列{an},a1=a,a2=b,且对满足m+n=p+q的正整数m,n,p,q都有=.
(1)当a=,b=时,求通项an;
(2)证明:对任意a,存在与a有关的常数λ,使得对于每个正整数n,都有≤an≤λ.
解:(1)由=
得=,
将a1=,a2=代入上式化简得an=,
所以=·.
故数列{}为等比数列,
从而=,即an=.
可验证,an=满足题设条件.
(2)由题设的值仅与m+n有关,记为bm+n,则bn+1==
考察函数f(x)=(x>0),
则在定义域上有f(x)≥g(a)=
故对n∈N*,bn+1≥g(a)恒成立.
又b2n=≥g(a),注意到0<g(a)≤,
解上式得:=≤an≤,
取λ=,即有≤an≤λ.
12.(15分)(2010·福建泉州一模)某城市决定对城区住房进行改造,在新建住房的同时拆除部分旧住房.第一年建新住房a m2,第二年到第四年,每年建设的新住房比前一年增长100%,从第五年起,每年建设的新住房都比前一年减少a m2;已知旧住房总面积为32a m2,每年拆除的数量相同.
(1)若10年后该城市住房总面积正好比改造前的住房总面积翻一番,则每年拆除的旧住房面积是多少m2?
(2)求前n(1≤n≤10且n∈N)年新建住房总面积Sn.
解:(1)10年后新建住房总面积为a+2a+4a+8a+7a+6a+5a+4a+3a+2a=42a.
设每年拆除的旧住房为x m2,
则42a+(32a-10x)=2×32a,
解得x=a,即每年拆除的旧住房面积是a m2.
(2)设第n年新建住房面积为a,
则an=
所以当1≤n≤4时,Sn=(2n-1)a;
当5≤n≤10时,Sn=a+2a+4a+8a+7a+6a+…+(12-n)a=15a+=,
故Sn=
11.(15分)已知等差数列{an}的前n项和为Sn,且a3=5,S15=225;数列{bn}是等比数列,b3=a2+a3,b2b5=128.
(1)求数列{an}的通项an及数列{bn}的前8项和T8;
(2)求使得>成立的正整数n.
解:(1)设等差数列{an}的公差为d,
由已知a1+2d=5,15a1+×15×14d=225,
即解得d=2,a1=1,
所以an=2n-1.
设等比数列{bn}的公比为q,
因为b3=a2+a3,所以b1q2=8,
因为b2b5=128,所以bq5=128,
解得q=2,b1=2,
T8==510.
(2)>即>,
解之得4<n<6,所以n=5.
10.设函数f(x)定义如下表,数列{xn}满足x0=5,且对任意自然数均有xn+1=f(xn),则x2006的值为__________.
|
x |
1 |
2 |
3 |
4 |
5 |
|
f(x) |
4 |
1 |
3 |
5 |
2 |
解析:∵x0=5,xn+1=f(xn),
∴x1=f(x0)=f(5)=2,x2=f(x1)=f(2)=1,
x3=f(x2)=f(1)=4,x4=f(x3)=f(4)=5.
从而知数列{xn}是以4为周期的数列,而x2006=f(x2005)=f(x1)=f(2)=1.
答案:1
9.已知数列{an}满足=(n∈N*),且a1=1,则an=__________.
解析:本题考查利用递推公式确定数列通项公式.据已知有:n≥2时利用累乘法得:an=a1···…·=1····…··=,又验证知a1=1也适合,故an=.
答案:
8.在等差数列{an}中,满足3a4=7a7,且a1>0,Sn是数列{an}前n项的和,若Sn取得最大值,则n=__________.
解析:设公差d,由题设3(a1+3d)=7(a1+6d),
所以d=-a1<0.
解不等式an>0,即a1+(n-1)(-a1)>0,所以n<,则n≤9,
当n≤9时,an>0,同理可得n≥10时,an<0.
故当n=9时,Sn取得最大值.
答案:9
7.有这样一首诗:“有个学生资性好,一部《孟子》三日了,每日添增一倍多,问君每日读多少?”(注:《孟子》全书共34685字,“一倍多”指一倍),由此诗知该君第二日读的字数为__________.
解析:设第一日读的字数为a,由“每日添增一倍多”得此数列是以a为首项,2为公比的等比数列,可求得三日共读的字数为=7a=34685,解得a=4955,∴2a=9910,即该君第二日读的字数为9910.
答案:9910
6.已知数列{an}的通项公式an=3n2-(9+a)n+6+2a(其中a为常数),若a6与a7两项中至少有一项是an的最小值,则实数a的取值范围是
( )
A.[24,36]
B.[27,33]
C.{a|27≤a≤33,a∈N*}
D.{a|24≤a≤36,a∈N*}
解析:设f(x)=3x2-(9+a)x+6+2a,其对称轴为x=,当≤≤时,即24≤a≤36时,a6与a7至少有一项是an的最小值.
答案:A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com