
题目列表(包括答案和解析)
5、不等式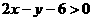 表示的平面区域在直线
表示的平面区域在直线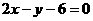 的( )
的( )
A.左上方 B.右上方 C.左下方 D.左下方
4、已知直线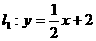 ,直线
,直线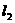 过点
过点 ,且
,且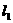 到
到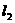 的夹角为
的夹角为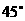 ,则直线
,则直线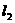 的方程是( )
的方程是( )
A.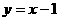 B.
B.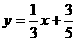 C.
C.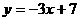 D.
D.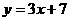
3、直线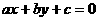 同时要经过第一、第二、第四象限,则
同时要经过第一、第二、第四象限,则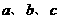 应满足( )
应满足( )
A.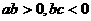 B.
B.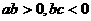 C.
C.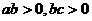 D.
D.
2、若圆C与圆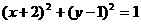 关于原点对称,则圆C的方程是( )
关于原点对称,则圆C的方程是( )
A.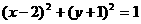 B.
B.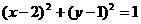
C.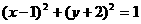 D.
D.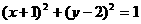
1、在直角坐标系中,直线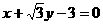 的倾斜角是( )
的倾斜角是( )
A.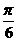 B.
B.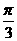 C.
C.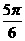 D.
D.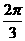
17) 已知椭圆C的焦点F1(- ,0)和F2(
,0)和F2( ,0),长轴长6,设直线
,0),长轴长6,设直线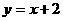 交椭圆C于A、B两点,求线段AB的中点坐标。(8分)
交椭圆C于A、B两点,求线段AB的中点坐标。(8分)
18) 已知双曲线与椭圆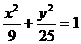 共焦点,它们的离心率之和为
共焦点,它们的离心率之和为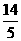 ,求双曲线方程.(10分).
,求双曲线方程.(10分).
19) 抛物线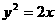 上的一点P(x , y)到点A(a,0)(a∈R)的距离的最小值记为
上的一点P(x , y)到点A(a,0)(a∈R)的距离的最小值记为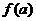 ,求
,求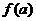 的表达式(10分)
的表达式(10分)
20)求两条渐近线为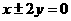 且截直线
且截直线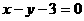 所得弦长为
所得弦长为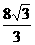 的双曲线方程。(10分)
的双曲线方程。(10分)
21)已知直线y=ax+1与双曲线3x2-y2=1交于A、B两点,(1)若以AB线段为直径的圆过坐标原点,求实数a的值。(2)是否存在这样的实数a,使A、B两点关于直线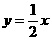 对称?说明理由。(10分)
对称?说明理由。(10分)
13)与椭圆 具有相同的离心率且过点(2,-
具有相同的离心率且过点(2,-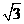 )的椭圆的标准方程是_____
)的椭圆的标准方程是_____
14)离心率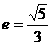 ,一条准线为
,一条准线为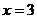 的椭圆的标准方程是_______。
的椭圆的标准方程是_______。
15)过抛物线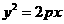 (p>0)的焦点F作一直线l与抛物线交于P、Q两点,作PP1、QQ1垂直于抛物线的准线,垂足分别是P1、Q1,已知线段PF、QF的长度分别是a、b,那么|P1Q1|= 。
(p>0)的焦点F作一直线l与抛物线交于P、Q两点,作PP1、QQ1垂直于抛物线的准线,垂足分别是P1、Q1,已知线段PF、QF的长度分别是a、b,那么|P1Q1|= 。
16)若直线l过抛物线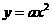 (a>0)的焦点,并且与y轴垂直,若l被抛物线截得的线段长为4,则a=_______。
(a>0)的焦点,并且与y轴垂直,若l被抛物线截得的线段长为4,则a=_______。
1)如果实数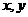 满足等式
满足等式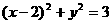 ,那么
,那么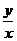 的最大值是( )
的最大值是( )
A、 B、
B、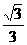 C、
C、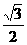 D、
D、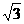
2)若直线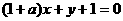 与圆
与圆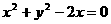 相切,则
相切,则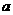 的值为( )
的值为( )
A、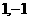 B、
B、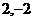 C、
C、 D、
D、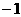
3)已知椭圆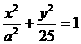
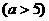 的两个焦点为
的两个焦点为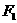 、
、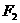 ,且
,且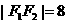 ,弦AB过点
,弦AB过点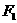 ,则△
,则△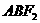 的周长为( )(A)10 (B)20
(C)2
的周长为( )(A)10 (B)20
(C)2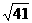 (D)
(D) 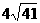
4)椭圆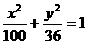 上的点P到它的左准线的距离是10,那么点P 到它的右焦点的距离是( )(A)15 (B)12 (C)10 (D)8
上的点P到它的左准线的距离是10,那么点P 到它的右焦点的距离是( )(A)15 (B)12 (C)10 (D)8
5)椭圆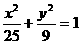 的焦点
的焦点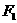 、
、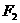 ,P为椭圆上的一点,已知
,P为椭圆上的一点,已知 ,则△
,则△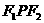 的面积为( )(A)9 (B)12 (C)10 (D)8
的面积为( )(A)9 (B)12 (C)10 (D)8
6)椭圆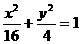 上的点到直线
上的点到直线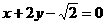 的最大距离是( )
的最大距离是( )
(A)3(B)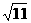 (C)
(C) (D)
(D)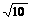
7)以坐标轴为对称轴、渐近线互相垂直、两准线间距离为2的双曲线方程是( )
(A)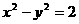 (B)
(B)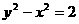
(C)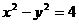 或
或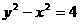 (D)
(D)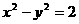 或
或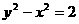
8)双曲线 右支点上的一点P到右焦点的距离为2,则P点到左准线的距离为( )
右支点上的一点P到右焦点的距离为2,则P点到左准线的距离为( )
(A)6 (B)8 (C)10 (D)12
9)过双曲线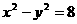 的右焦点F2有一条弦PQ,|PQ|=7,F1是左焦点,那么△F1PQ的周长为( )(A)28 (B)
的右焦点F2有一条弦PQ,|PQ|=7,F1是左焦点,那么△F1PQ的周长为( )(A)28 (B)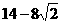 (C)
(C) (D)
(D)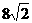
10)双曲线虚轴上的一个端点为M,两个焦点为F1、F2,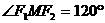 ,则双曲线的离心率为( )(A)
,则双曲线的离心率为( )(A)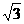 (B)
(B)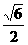 (C)
(C)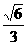 (D)
(D)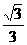
11)过抛物线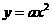 (a>0)的焦点F作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别为p、q,则
(a>0)的焦点F作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别为p、q,则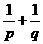 等于( )
等于( )
(A)2a
(B)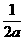 (C)
(C)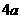
 (D)
(D)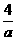
12) 如果椭圆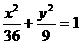 的弦被点(4,2)平分,则这条弦所在的直线方程是( )
的弦被点(4,2)平分,则这条弦所在的直线方程是( )
(A)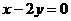 (B)
(B)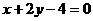 (C)
(C)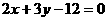 (D)
(D)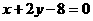
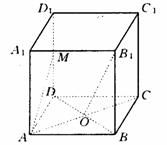
24、在正方体ABCD-A1B1C1D1中,O为正方形ABCD的中心,M为D1D的中点.
(I)求证:异面直线B1O与AM垂直;
(II)求二面角B1-AM-C的大小;
(III)若正方体的棱长为a,求三棱锥B1-AMC的体积。(9分)
23、如图,正方形ACC1A1与等腰直角△ACB互相垂直,∠ACB=90°,E、F分别是AB、BC的中点, G是AA1上的点.
(I)若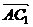

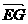 ,试确定点G的位置;
,试确定点G的位置;
(II)在满足条件(1)的情况下,试求cos<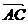 ,
,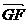 >的值.(8分)
>的值.(8分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com