
题目列表(包括答案和解析)
19.(本小题满分12分)为了能更好地了解鲸的生活习性,某动物研究所在受伤的鲸身上安装了电子监测装置,从海岸放归点A处(如图所示)把它放归大海,并沿海岸线由西到东不停地对鲸进行了40分钟的跟踪观测,每隔10分钟踩点测得数据如下表(设鲸沿海面游动)。然后又在观测站B处对鲸进行生活习性的详细观测。已知AB=15km,观测站B的观测半径为5km.
|
观测时刻t(分钟) |
跟踪观测点到放归点距离a(km) |
鲸位于跟踪观测点正北方向的距离b(km) |
|
10 |
1 |
1 |
|
20 |
2 |
|
|
30 |
3 |
|
|
40 |
4 |
2 |
(I)根据表中数据:(1)计算鲸沿海岸线方向运动的速度,(2)写出a、b满足的关系式
并画出鲸的运动路线简图;
(II)若鲸继续以(I)-(2)中的运行路线运动,则鲸经过多少分钟(从放归时计时),
可进入前方观测站B的观测范围。
18.(本小题满分12分)如图所示,已知四面体O-ABC中, M 为BC的中点,N为AC
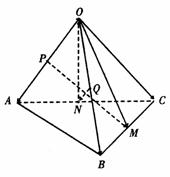 的中点,Q为OB的中点,P为OA的中点,若AB=OC,试用向量方法证明,PM⊥QN.
的中点,Q为OB的中点,P为OA的中点,若AB=OC,试用向量方法证明,PM⊥QN.
17.(本小题满分12分)已知函数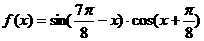 的图象向右平移个单位得到函数
的图象向右平移个单位得到函数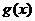 的图象.
的图象.
(I)求函数g(x)的表达式;
(II)证明当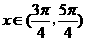 时,经过函数g(x)图象上任意两点的直线的斜率恒大于零.
时,经过函数g(x)图象上任意两点的直线的斜率恒大于零.
16.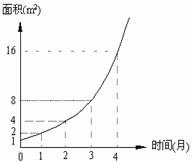 某池塘中野生水葫芦的面积与时间的函数关系的图象,如右图所示. 假设其关系为指数函数,并给出下列说法
某池塘中野生水葫芦的面积与时间的函数关系的图象,如右图所示. 假设其关系为指数函数,并给出下列说法
①此指数函数的底数为2;
②在第5个月时,野生水葫芦的面积就会超过30m2;
③野生水葫芦从4m2蔓延到12m2只需1.5个月;
④设野生水葫芦蔓延到2m2,3m2, 6m2所需的时间分别
为t1, t2, t3, 则有t1 + t2 = t3;
⑤野生水葫芦在第1到第3个月之间蔓延的平均速度
等于在第2到第4个月之间蔓延的平均速度.
其中正确的说法有 . (请把正确说法的序号都填在横线上)
15.若z=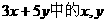 满足约束条件
满足约束条件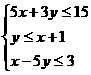 ,则Z的最大值和最小值分别为
,则Z的最大值和最小值分别为
.
14.已知偶函数 的图象与
的图象与 轴有五个公共点,那么方程
轴有五个公共点,那么方程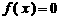 的所有实根之和为
的所有实根之和为
_______.
13.若复数z满足的最小值是___________.
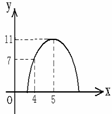
12.某企业购置了一批设备投入生产,据分析每台设备生产的总利
润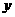 (单位:万元)与年数
(单位:万元)与年数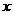
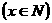 满足如图的二次函数关系。
满足如图的二次函数关系。
要使生产的年平均利润最大,则每台设备应使用 ( )
A.3年 B.4年 C.5年 D.6年
11.若直线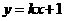 与曲线
与曲线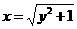 有两个不同的交点,则
有两个不同的交点,则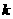 的取值范围是 ( )
的取值范围是 ( )
A.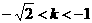 B.
B.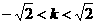
 C.
C.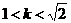 D.
D.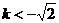 或
或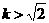
10.四面体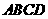 的六条棱中,其中五条棱的长度都是2,则第六条棱长的取值范围是( )
的六条棱中,其中五条棱的长度都是2,则第六条棱长的取值范围是( )
A.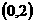 B.
B.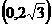 C.
C.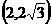 D.
D.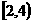
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com