12．己知f(x)＝－x³－x，x ∈[m，n]，且f(m)·f(n)＜0，则方程f(x)＝0在区间[m，n]上(　)

A．至少有三个实数根

B．至少有两个实根

C．有且只有一个实数根

D．无实根

答案：C

解析：∵f ′(x)＝－3x²－1＜0，

∴f(x)在区间[m，n]上是减函数，又f(m)·f(n)＜0，故方程f(x)＝0在区间[m，n]上有且只有一个实数根．

第Ⅱ卷(非选择题　共90分)

11．要做一个圆锥形漏斗，其母线长为20cm，要使其体积最大，其高应为　　　 (　)

A.cm　 　　　　　　　　　　　　　　　 B．100cm

C．20cm　 　　　　　　　　　　　　　　　　 D.cm

答案：A

解析：设高为h，则半径为，

体积V＝πr²h＝π(20²－h²)·h

＝－πh³+πh(0＜h＜20)，

V′＝－πh²+π.

令V′＝0，得h＝或h＝－(舍去)，

即当h＝时，V为最大值．

10．(2010·北京师大附中)已知函数f(x)＝x²+bx的图象在点A(1，f(1))处的切线斜率为3，数列{}的前n项为S_n则S₂₀₁₁的值为　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.　 　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　 D.

答案：A

解析：∵f ′(x)＝2x+b，f ′(1)＝2+b＝3，∴b＝1，

∴f(x)＝x²+x，∴＝＝＝－，

∴S₂₀₁₁＝(1－)+(－)+…+(－)＝，故选A.

9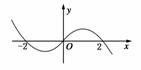．已知函数f(x)是定义在R上的函数，如果函数f(x)在R上的导函数f ′(x)的图象如图，则有以下几个命题：

(1)f(x)的单调递减区间是(－2,0)、(2，+∞)，

f(x)的单调递增区间是(－∞，－2)、(0,2)；

(2)f(x)只在x＝－2处取得极大值；

(3)f(x)在x＝－2与x＝2处取得极大值；

(4)f(x)在x＝0处取得极小值．

其中正确命题的个数为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．1　 　　　　　　　　　　　　　　　　　　　 B．2

C．3　 　　　　　　　　　　　　　　　　　　　 D．4

答案：C

解析：由图知，当x＜－2或0＜x＜2时，f ′(x)＞0；

当－2＜x＜0或x＞2时，f ′(x)＜0，所以(1)、(3)、(4)正确．

8．设函数f(x)＝ax³+bx²+cx在x＝±1处均有极值，且f(－1)＝－1，则a，b，c的值为(　)

A．a＝－，b＝0，c＝－

B．a＝，b＝0，c＝－

C．a＝－，b＝0，c＝

D．a＝，b＝0，c＝

答案：C

解析：f ′(x)＝3ax²+2bx+c，

由题知⇒，

∴

7．(2009·甘肃省河西五市联考)设函数f(x)是R上以5为周期的可导偶函数，则曲线y＝f(x)在x＝5处的切线的斜率为　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　 (　)

A．－　　　　　　　　　　　 B．0

C.　 　　　　　　　　　　　　　　　　　　　　 D．5

答案：B

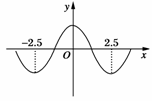
解析：可把f(x)的图象想象成下图．

∴y′|_x＝5＝0.

6．(2009·苏州四市高三调研)已知曲线y＝的一条切线的斜率为，则切点的横坐标为

(　)

A．1　　　　　　　　　　 B．2

C．3　 　　　　　　　　　　　　　　　　　　　 D．4

答案：A

解析：∵y′＝＝，∴x＝1.

5．函数f(x)＝2x³－3x²－12x+5在[0,3]上的最大值和最小值分别是　　　　　　　　　 (　)

A．12，－15　 B．－4，－15

C．12，－4　 D．5，－15

答案：D

解析：f ′(x)＝6x²－6x－12，令f ′(x)＝0得x＝－1或x＝2，∵f(0)＝1，f(2)＝－15，f(3)＝－4，

∴f(x)_max＝5，f(x)_min＝－15，故选D.

4．函数y＝x³－3x²－9x+14的单调区间为　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．在(－∞，－1)和(－1,3)内单调递增，在(3，+∞)内单调递减

B．在(－∞，－1)内单调递增，在(－1,3)和(3，+∞)内单调递减

C．在(－∞，－1)和(3，+∞)内单调递增，在(－1,3)内单调递减

D．以上都不对

答案：C

解析：y′＝3x²－6x－9＝3(x²－2x－3)＝3(x+1)(x－3)，

令y′＞0得x＜－1或x＞3，

故增区间为(－∞，－1)，(3，+∞)．

令y′＜0得－1＜x＜3，

故减区间为(－1,3)．

3．(2009·郑州市高中毕业班第一次质量预测试卷)曲线y＝x³+x－2在点A(1,0)处的切线方程是　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．4x－y＝0　　　　　 B．4x－y－2＝0

C．4x－y－4＝0　 　　　　　　　 D．4x+y－4＝0

答案：C

解析：依题意得y′＝3x²+1，因此曲线y＝x³+x－2在点A(1,0)处的切线的斜率等于4，相应的切线方程是y＝4(x－1)，即4x－y－4＝0，选C.