22．(2009·福建，21)(本小题满分12分)已知函数f(x)＝x³+ax²+bx，且f ′(－1)＝0.

(1)试用含a的代数式表示b；

(2)求f(x)的单调区间；

(3)令a＝－1，设函数f(x)在x₁、x₂(x₁＜x₂)处取得极值，记点M(x₁，f(x₁))，N(x₂，f(x₂))．证明：线段MN与曲线f(x)存在异于M，N的公共点．

命题意图：本小题主要考查函数、导数等基础知识，考查推理论证能力、运算求解能力，考查函数与方程思想、数形结合思想、化归与转化思想、分类与整合思想．

解析：解法一：(1)依题意，得

f ′(x)＝x²+2ax+b.

由f ′(－1)＝1－2a+b＝0得b＝2a－1.

(2)由(1)得f(x)＝x³+ax²+(2a－1)x，故f ′(x)＝x²+2ax+2a－1＝(x+1)(x+2a－1)．

令f ′(x)＝0，则x＝－1或x＝1－2a.

①当a＞1时，1－2a＜－1.

当x变化时，f ′(x)与f(x)的变化情况如下表：

由此得，函数f(x)的单调增区间为(－∞，1－2a)和(－1，+∞)，单调减区间为(1－2a，－1)．

②当a＝1时，1－2a＝－1.此时，f ′(x)≥0恒成立，且仅在x＝－1处f ′(x)＝0，故函数f(x)的单调增区间为R.

③当a＜1时，1－2a＞－1，同理可得函数f(x)的单调增区间为(－∞，－1)和(1－2a，+∞)，单调减区间为(－1,1－2a)．

综上所述：当a＞1时，函数f(x)的单调增区间为(－∞，1－2a)和(－1，+∞)，单调减区间为(1－2a，－1)；

当a＝1时，函数f(x)的单调增区间为R；

当a＜1时，函数f(x)的单调增区间为(－∞，－1)和(1－2a，+∞)，单调减区间为(－1,1－2a)．

(3)当a＝－1时，得f(x)＝x³－x²－3x.

由f ′(x)＝x²－2x－3＝0，得x₁＝－1，x₂＝3.

由(2)得f(x)的单调增区间为(－∞，－1)和(3，+∞)，单调减区间为(－1,3)，所以函数f(x)在x₁＝－1，x₂＝3处取得极值．故M(－1，)，N(3，－9)．

所以直线MN的方程为y＝－x－1.

由得x³－3x²－x+3＝0.

令F(x)＝x³－3x²－x+3.

易得F(0)＝3＞0，F(2)＝－3＜0，而F(x)的图象在(0,2)内是一条连续不断的曲线，故F(x)在(0,2)内存在零点x₀，这表明线段MN与曲线f(x)有异于M，N的公共点．

解法二：(1)同解法一．

(2)同解法一．

(3)当a＝－1时，得f(x)＝x³－x²－3x.

由f ′(x)＝x²－2x－3＝0，得x₁＝－1，x₂＝3.

由(2)得f(x)的单调增区间为(－∞，－1)和(3，+∞)，单调减区间为(－1,3)，所以函数f(x)在x₁＝－1，x₂＝3处取得极值，

故M(－1，)，N(3，－9)．

所以直线MN的方程为y＝－x－1.

由得x³－3x²－x+3＝0.

解得x₁＝－1，x₂＝1，x₃＝3.

∴

所以线段MN与曲线F(x)有异于M，N的公共点(1，－)．

21．(2010·河南省实验中学期中试卷)(本小题满分12分)已知函数f(x)＝ax³+bx²－3x在x＝±1处取得极值．

(1)求函数f(x)的解析式；

(2)求证：对于区间[－1,1]上任意两个自变量x₁、x₂都有|f(x₁)－f(x₂)|≤4；

(3)若过点A(1，m)(m≠－2)可作曲线y＝f(x)的三条切线，求实数m的取值范围．

解析：(1)∵f ′(x)＝3ax²+2bx－3，

依题意f ′(1)＝f ′(－1)＝0，

即，解得a＝1，b＝0，∴f(x)＝x³－3x.

(2)∵f(x)＝x³－3x，∴f ′(x)＝3x²－3＝3(x+1)(x－1)，

当－1＜x＜1时，f ′(x)＜0，故f(x)在区间[－1,1]上为减函数，

f_max(x)＝f(－1)＝2，f_min(x)＝f(1)＝－2，

∵对于区间[－1,1]上任意两个自变量x₁、x₂

都有|f(x₁)－f(x₂)|≤|f_max(x)－f_min(x)|

即|f(x₁)－f(x₂)|≤|2－(－2)|＝4.

(3)f ′(x)＝3x²－3＝3(x+1)(x－1)，

∵曲线方程为f(x)＝x³－3x，∴点A(1，m)不在曲线上，

设切点为M(x₀，y₀)，则点M的坐标满足y₀＝x－3x₀，

因f ′(x₀)＝3(x－1)，故切线的斜率为3(x－1)＝，整理得2x－3x+m+3＝0.

∵过点A(1，m)可作三条切线，

∴关于x₀的方程式2x－3x+m+3＝0有三个实根，设g(x₀)＝2x－3x+m+3，

则g′(x₀)＝6x－6x₀由g′(x₀)＝0得x₀＝0或x₀＝1，

∴函数g(x₀)＝2x－3x+m+3的极值点为x₀＝0，x₀＝1，

∴关于x₀的方程2x－3x+m+3＝0有三个实数根的充要条件是g(1)g(0)＜0即(m+3)(m+2)＜0，

解得－3＜m＜－2，故所求实数a的取值范围是－3＜m＜－2.

20．(本小题满分12分)函数f(x)＝x³+ax²+bx+c，过曲线y＝f(x)上的点P(1，f(1))的切线方程为y＝3x+1.

(1)若y＝f(x)在x＝－2时有极值，求f(x)的表达式；

(2)在(1)的条件下，求y＝f(x)在[－3,1]上的最大值．

解析：(1)由f(x)＝x³+ax²+bx+c，求导数得f ′(x)＝3x²+2ax+b，过y＝f(x)上的点P(1，f(1))的切线方程为：y－f(1)＝f ′(1)(x－1)，即为：y－(a+b+c+1)＝(3+2a+b)(x－1)，而过P(1，f(1))的切线方程是y＝3x+1，∴　①

又y＝f(x)在x＝－2时有极值，∴f ′(－2)＝0，∴－4a+b＝－12，　②

联立方程组得：a＝2，b＝－4，c＝5，

即f(x)＝x³+2x²－4x+5.

(2)f ′(x)＝3x²+4x－4＝(3x－2)(x+2)，

f(x)、 f ′(x)的变化如下表：

f(x)_极大值＝f(－2)＝13，又f(1)＝4，

∴f(x)在区间[－3,1]上的最大值是13.

19．(2009·北京市东城区高三示范学校质量检测)(本小题满分12分)已知函数f(x)＝x³+ax²+bx+c在x＝－与x＝1时都取得极值．

(1)求a、b的值与函数f(x)的单调区间；

(2)若对x∈[－1,2]，不等式f(x)＜c²恒成立，求c的取值范围．

解析：(1)∵f(x)＝x³+ax²+bx+c，

∴f ′(x)＝3x²+2ax+b.由

，

解得，∴f ′(x)＝3x²－x－2＝(3x+2)(x－1)，

函数f(x)的单调区间如下表：

所以函数f(x)的递增区间是(－∞，－)与(1，+∞)，递减区间是(－，1)．

(2)由f(x)＝x³－x²－2x+c，x∈[－1,2]，

当x＝－时，f(x)＝+c为极大值，而f(2)＝2+c，

所以f(2)＝2+c为最大值．

要使f(x)＜c²对x∈[－1,2]恒成立，须且只需c²＞f(2)＝2+c.解得c＜－1或c＞2.

18．(2009·山东青岛一模)(本小题满分12分)已知函数f(x)＝ax³－3x²+1－(a∈R且a≠0)，试求函数f(x)的极大值与极小值．

解析：由题设知a≠0，f ′(x)＝3ax²－6x＝3ax(x－)，令f ′(x)＝0得x＝0或x＝.

当a＞0时，随x的变化，f ′(x)与f(x)的变化如下表：

∴f(x)_极大值＝f(0)＝1－，

f(x)_极小值＝f()＝－－+1.

当a＜0时，随x的变化，f ′(x)与f(x)的变化如下表：

∴f(x)_极大值＝f(0)＝1－，

f(x)_极小值＝f()＝－－+1.

总之，当a＞0时，f(x)_极大值＝f(0)＝1－，

f(x)_极小值＝f()＝－－+1；

当a＜0时，f(x)_极大值＝f(0)＝1－，

f(x)_极小值＝f()＝－－+1.

17．(本小题满分10分)已知函数f(x)＝x³－3ax，

(1)求函数f(x)的单调区间；

(2)当a＝1时，求证：直线4x+y+m＝0不可能是函数f(x)图象的切线．

解析：(1)∵f ′(x)＝3x²－3a＝3(x²－a)，

当a≤0时，f ′(x)＝3x²－3a≥0对x∈R恒成立，

∴f(x)的递增区间为(－∞，+∞)．

当a＞0时，由f ′(x)＞0，得x＜－或x＞，

由f ′(x)＜0，得－＜x＜.

此时，f(x)的递增区间是(－∞，－)和(，+∞)；

递减区间是(－，)．

(2)证明：∵a＝1，∴f ′(x)＝3x²－3.

直线4x+y+m＝0的斜率为－4，假设f ′(x)＝－4，即3x²+1＝0.

此方程无实根，∴直线4x+y+m＝0不可能是函数f(x)图象的切线．

16．若函数f(x)＝x³－mx²+2m²－5的单调递减区间为(－9,0)，则m＝________.

答案：－

解析：f ′(x)＝3x²－2mx.

法一：令f ′(x)＜0则3x²－2mx＜0.

若m＞0，则0＜x＜与单调递减区间为(－9,0)矛盾．

若m＜0，则m＜x＜0，

∴－9＝m，∴m＝－.

法二：令f ′(x)＜0，则3x²－2mx＜0，

由题意得，不等式的解集为(－9,0)，

∴－9,0是方程3x²－2mx＝0的两个根．

∴－9+0＝－，∴m＝－.

15．已知f(x)＝x³+3x²+a(a为常数)，在[－3,3]上有最小值3，那么在[－3,3]上f(x)的最大值是________．

答案：57

解析：本题考查导数的应用f ′(x)＝3x²+6x，令f ′(x)＝0，得3x(x+2)＝0⇒x＝0，x＝－2.i)当0≤x≤3，或－3≤x≤－2时，f ′(x)≥0，f(x)单调递增，ii)当－2<x<0时，f(x)单调递减，由最小值为3知，最小为f(－3)或f(0)⇒f(－3)＝(－3)³+3×(－3)²+a＝a，f(0)＝a，则a＝3，∴f(x)＝x³+3x²+3，其最大值为f(－2)或f(3)，f(－2)＝(－2)³+3×(－2)²+3＝7，f(3)＝3³+3×3²+3＝57，则最大值为57.

14．(2009·河北三市联测)曲线y＝x³+x－2的一条切线平行于直线y＝4x－1，则切点P₀的坐标为______________．

答案：(1,0)或(－1，－4)

解析：由y＝x³+x－2，得y′＝3x²+1，由已知得3x²+1＝4，解之得x＝±1.当x＝1时，y＝0；当x＝－1时，y＝－4.

∴切点P₀的坐标为(1,0)或(－1，－4)．

点评：利用导数研究函数的性质是导数的重要应用之一，导数的广泛应用为我们解决函数问题提供了有力的帮助．本小题主要考查利用导数求切点的坐标．

13．(1)如图，函数f(x)的图象是折线段ABC，其中A，B，C的坐标分别为(0,4)，(2,0)，(6,4)，则f(f(0))＝________；

(2)函数f(x)在x＝1处的导数f ′(1)＝________.

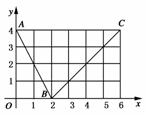
答案：(1)2　(2)－2

解析：(1)由图及题中已知可得f(x)＝

，f(0)＝4，

则f(f(0))＝f(4)＝2.

(2)f ′(1)＝－2.