
题目列表(包括答案和解析)
80. 已知:平面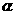 与平面
与平面 相交于直线a,直线b与
相交于直线a,直线b与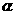 、
、 都平行,求证:b∥a.
都平行,求证:b∥a.
证明:在a上取点P,b和P确定平面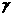 设
设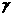 与
与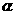 交于
交于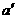 ,
,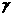 与
与 交于
交于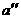
∵ b∥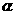 且b∥
且b∥
∴ b∥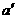 且b∥
且b∥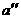
∴ 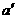 与
与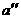 重合,而
重合,而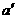
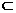
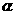 ,
,
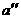
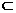
 ,实际上是
,实际上是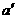 、
、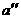 、a三线重合,
、a三线重合,
∴ a∥b.
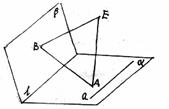
79. 如图,已知a、b是两条相互垂直的异面直线,其公垂线段AB的长为定值m,定长为n(n>m)的线段PQ的两个端点分别在a、b上移动,M、N分别是AB、PQ的中点。
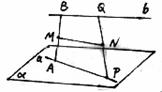 (1)求证:AB⊥MN;
(1)求证:AB⊥MN;
(2)求证:MN的长是定值(14分)
解析:

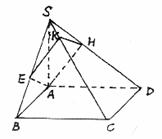
78. 在正方体ABCD-A1B1C1D1,G为CC1的中点,O为底面ABCD的中心。
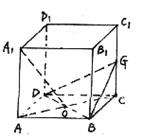 求证:A1O⊥平面GBD(14分)
求证:A1O⊥平面GBD(14分)
解析:
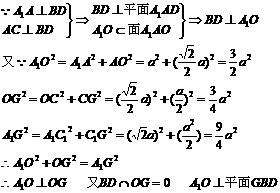
77. .如图,ABCD为正方形,过A作线段SA⊥面ABCD,又过A作与SC垂直的平面交SB、SC、SD于E、K、H,求证:E、H分别是点A在直线SB和SD上的射影。(12分)
解析:

76. 如图,已知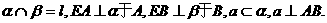
求证a∥l
解析:
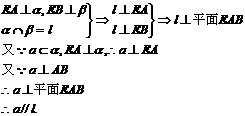
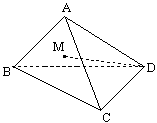
75. 设P、Q是单位正方体AC1的面AA1D1D、面A1B1C1D1的中心。
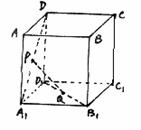 如图:(1)证明:PQ∥平面AA1B1B;
如图:(1)证明:PQ∥平面AA1B1B;
(2)求线段PQ的长。(12分)

评注:本题提供了两种解法,方法一,通过平行四边形的对边平行得到“线线平行”,从而证得“线面平行”;方法二,通过三角形的中位线与底边平行得到“线线平行”,从而证得“线面平行”。本题证法较多。
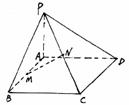
74. 已知PA⊥矩形ABCD所在平面,M、N分别是AB、PC的中点.
(1)求证:MN⊥CD;
(2)若∠PDA=45°,求证MN⊥面PCD.(12分)
解析:
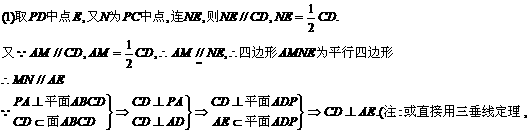
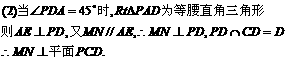
71. 球面上有三个点A、B、C. A和B,A和C间的球面距离等于大圆周长的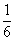 .
B和C间的球面距离等于大圆周长的
.
B和C间的球面距离等于大圆周长的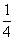 .如果球的半径是R,那么球心到截面ABC的距离等于
.如果球的半径是R,那么球心到截面ABC的距离等于
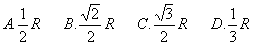 解析:本题考查球面距离的概念及空间想像能力.
解析:本题考查球面距离的概念及空间想像能力.
如图所示,圆O是球的大圆,且大圆所在平面与面ABC垂直,其中弦EF是过A、B、C的小圆的直径,弦心距OD就是球心O到截面ABC的距离,OE是球的半径,因此,欲求OD,需先求出截面圆ABC的半径. 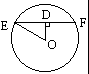
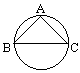
下一个图是过A、B、C的小圆.AB、AC、CB是每两点之间的直线段.它们的长度要分别在△AOB、△AOC、△COB中求得(O是球心).由于A、B间球面距离是大圆周长的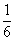 ,所以∠AOB=
,所以∠AOB=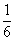 ×2π=
×2π=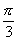 ,同理∠AOC=
,同理∠AOC=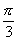 ,∠BOC=
,∠BOC=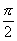 .
. 
∴|AB|=R, |AC|=R, |BC|=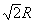 .
在△ABC中,由于AB2+AC2=BC2.
∴∠BAC=90°,BC是小圆ABC的直径.
∴|ED|=
.
在△ABC中,由于AB2+AC2=BC2.
∴∠BAC=90°,BC是小圆ABC的直径.
∴|ED|=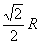 从而|OD|=
从而|OD|=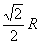 .
故应选B.
72. 如图,四棱锥P-ABCD中,ABCD是正方形,PA⊥底面ABCD,该图中,互相垂直的面有
A.4对 B.5对 C.6对 D.7对
.
故应选B.
72. 如图,四棱锥P-ABCD中,ABCD是正方形,PA⊥底面ABCD,该图中,互相垂直的面有
A.4对 B.5对 C.6对 D.7对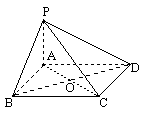 答案(D)
解析:要找到一个好的工作方法,使得计数时不至于产生遗漏
73. ABCD是各条棱长都相等的三棱锥.M是△ABC的垂心,那么AB和DM所成的角等于______
答案(D)
解析:要找到一个好的工作方法,使得计数时不至于产生遗漏
73. ABCD是各条棱长都相等的三棱锥.M是△ABC的垂心,那么AB和DM所成的角等于______
解析:90°连CM交AB于N,连DN,易知N是AB中点,AB⊥CN,AB⊥DN.
70. 将边长为1的正方形ABCD,沿对角线AC折起,使BD=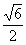 .则三棱锥D-ABC的体积为
.则三棱锥D-ABC的体积为

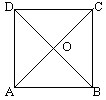
解析:设AC、BD交于O点,则BO⊥AC
且DO⊥AC,在折起后,这个垂直关系不变,因此∠BOD是二面角B-AC-D的平面角.
由于△DOB中三边长已知,所以可求出∠BOD:
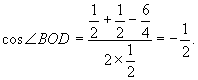
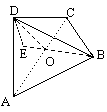
这是问题的一方面,另一方面为了求体积,应求出高,这个高实际上是△DOB中,OB边上的高DE,理由是:
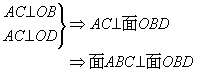 ∵DE⊥OB
∴DE⊥面ABC.
∵DE⊥OB
∴DE⊥面ABC. 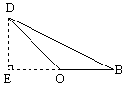
由cos∠DOB=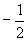 ,知sin∠DOE=
,知sin∠DOE=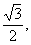 ∴DE=
∴DE=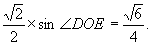 ∴
∴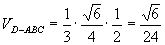 应选(B)
应选(B)
69. 如图,ABCD-A1B1C1D1是正方体,E、F分别是AD、DD1的中点,则面EFC1B和面BCC1所成二面角的正切值等于
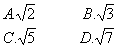 解析:为了作出二面角E-BC1-C的平面角,需在一个面内取一点,过该点向另一个面引垂线(这是用三垂线定理作二面角的平面角的关键步骤)。
解析:为了作出二面角E-BC1-C的平面角,需在一个面内取一点,过该点向另一个面引垂线(这是用三垂线定理作二面角的平面角的关键步骤)。 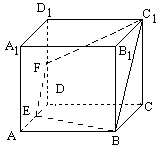
从图形特点看,应当过E(或F)作面BCC1的垂线.
解析:过E作EH⊥BC,垂足为H. 过H作HG⊥BC1,垂足为G.连EG.
∵面ABCD⊥面BCC1,而EH⊥BC
∵EH⊥面BEC1,
EG是面BCC1的斜线,HG是斜线EG在面BCC1内的射影.
∵HG⊥BC1, 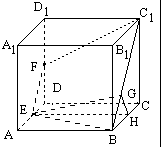
∴EG⊥BC1,
∴∠EGH是二面角E-BC1-C的平面角。
在Rt△BCC1中:sin∠C1BC=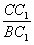 =
=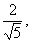 在Rt△BHG中:sin∠C1BC=
在Rt△BHG中:sin∠C1BC=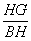 ∴HG=
∴HG=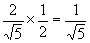 (设底面边长为1).
(设底面边长为1).
而EH=1,
在Rt△EHG中:tg∠EGH=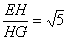 ∴∠EGH=arctg
∴∠EGH=arctg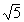 故二面角E-BC1-C 等于arctg
故二面角E-BC1-C 等于arctg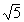 .
. 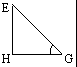
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com