21．(2009·郑州市高三2月份质检)(本小题满分12分)设函数f(x)＝x²+2bx+c，c＜b＜1，f(1)＝0且方程f(x)+1＝0有实数根．

(1)证明：－3＜c≤－1，且b≥0；

(2)若m是方程f(x)+1＝0的一个实数根，判断f(m－4)的符号，并证明你的结论．

解析：(1)∵f(1)＝0，∴1+2b+c＝0；

∴b＝－.

又c＜b＜1，

故c＜－＜1.即－3＜c＜－.

又f(x)+1＝0有实数根．

即x²+2bx+c+1＝0有实数根．

∴△＝4b²－4(c+1)≥0；

即(c+1)²－4(c+1)≥0；

∴c≥3或c≤－1；

又－3＜c＜－，取交集得－3＜c≤－1，

由b＝－知b≥0.

(2)f(x)＝x²+2bx+c

＝x²－(c+1)x+c

＝(x－c)(x－1)．

∴函数f(x)＝x²+2bx+c的图象与x轴交于A(c,0)、B(1,0)两点；

∵f(m)＝－1＜0，∴0＜m＜1；

∴c－4＜m－4＜1－4＜c；

∴m－4＜c.

∵f(x)＝x²+2bx+c在(－∞，c)上递减，

∴f(m－4)＞f(c)＝0.

∴f(m－4)的符号为正．

总结评述：本题属代数推理题．将二次函数、二次方程与不等式结合起来考查．探求二次函数背景下的不等式问题，实质是将二次函数的有关性质进行适当转化．

20．(2009·福建师大附中期末测试)(本小题满分12分)已知函数f(x)＝x²+(x≠0，常数a∈R)，

(1)讨论函数f(x)的奇偶性，并说明理由；

(2)若函数f(x)在x∈[2，+∞)上是增函数，求a的取值范围．

解析：(1)当a＝0时，f(x)＝x(x∈R且x≠0)，

∴f(－x)＝f(x)．∴f(x)是偶函数．

当a≠0时，∵f(－1)+f(1)＝2≠0，f(－1)－f(1)＝－2a≠0，

∴f(－1)≠±f(1)．∴f(x)是非奇非偶函数．

(2)依题意f′(x)＝2x－＝≥0在[2，+∞)上恒成立，

即2x³－a≥0在[2，+∞)上恒成立．

∴只要(2x³－a)_min＝16－a≥0.∴a≤16.

∴a的取值范围为(－∞，16]．

19．(本小题满分12分)已知二次函数y＝f(x)的定义域为R，f(1)＝2，在x＝t处取得最值，若y＝g(x)为一次函数，且f(x)+g(x)＝x²+2x－3.

(1)求f(x)的解析式；

(2)若x∈[－1,2]时，f(x)≥－1恒成立，求t的取值范围．

解析：(1)设f(x)＝a(x－t)²+b，

∵f(1)＝2，∴a(1－t)²+b＝2.

又f(x)+g(x)＝x²+2x－3，g(x)为一次函数，

∴a＝1，则b＝2－(1－t)²，

∴f(x)＝(x－t)²+2－(1－t)²＝(x－t)²－t²+2t+1.

(2)①若t＜－1时，

要使f(x)≥－1恒成立，只需f(－1)≥－1，

即t≥－，这与t＜－1矛盾；

②－1≤t≤2时，要使f(x)≥－1恒成立，

只需f(t)≥－1，即－t²+2t+1≥－1，

即1－≤t≤1+，∴1－≤t≤2；

③若t＞2时，要使f(x)≥－1恒成立，

只需f(2)≥－1，即t≤3，∴2＜t≤3，

综上所述t的取值范围是[1－，3]．

18．(本小题满分12分)设函数f(x)对任意x，y∈R，都有f(x+y)＝f(x)+f(y)，且x＞0，f(x)＜0；f(1)＝－2.

(1)证明f(x)是奇函数；

(2)证明f(x)在R上是减函数；

(3)求f(x)在区间[－3,3]上的最大值和最小值．

证明：(1)由f(x+y)＝f(x)+f(y)，

得f[x+(－x)]＝f(x)+f(－x)，

∴f(x)+f(－x)＝f(0)．

又f(0+0)＝f(0)+f(0)，∴f(0)＝0.

从而有f(x)+f(－x)＝0.∴f(－x)＝－f(x)．

∴f(x)是奇函数．

(2)任取x₁、x₂∈R，且x₁＜x₂，则f(x₁)－f(x₂)＝f(x₁)－f[x₁+(x₂－x₁)]＝f(x₁)－[f(x₁)+f(x₂－x₁)]＝－f(x₂－x₁)．由x₁＜x₂，

∴x₂－x₁＞0.∴f(x₂－x₁)＜0.

∴－f(x₂－x₁)＞0，即f(x₁)＞f(x₂)，

从而f(x)在R上是减函数．

(3)由于f(x)在R上是减函数，故f(x)在[－3,3]上的最大值是f(－3)，最小值为f(3)．由f(1)＝－2，得f(3)＝f(1+2)＝f(1)+f(2)＝f(1)+f(1+1)＝f(1)+f(1)+f(1)＝3f(1)＝3×(－2)＝－6，f(－3)＝－f(3)＝6.

∴最大值为6，最小值为－6.

17．(2009·山东潍坊统考)(本小题满分10分)已知函数f(x)＝－(a＞0)，若f(x)的定义域和值域都是[，2]，求实数a的值．

解：设≤x₁＜x₂≤2，则x₁－x₂＜0，x₁x₂＞0，

f(x₁)－f(x₂)＝(－)－(－)＝－＝＜0，f(x₁)＜f(x₂)，即f(x)在[，2]上是单调递增函数．

∵f(x)的定义域、值域都是[，2]，

又f(x)在[，2]上是单调增函数，

∴即∴a＝.

16．设函数f(x)＝lg(x²+ax－a－1)，给出如下命题：

①函数f(x)必有最小值；

②若a＝0时，则函数f(x)的值域是R；

③若a＞0，且f(x)的定义域为[2，+∞)，则函数f(x)有反函数；

④若函数f(x)在区间[2，+∞)上单调递增，则实数a的取值范围是[－4，+∞)．

其中正确的命题序号是______________．(将你认为正确的命题序号都填上)

答案：②③

解析：令u＝x²+ax－a－1＝(x+)²－－a－1≥－－a－1.

又u＞0，故u没有最小值，所以①错误；

当a＝0时，u＝x²－1∈[－1，+∞)，

而(0，+∞)⊆[－1，+∞)，所以②正确；

当a＞0时，u＝x²+ax－a－1的对称轴为x＝－＜0，[2，+∞)为单调递增区间，

当x∈[2，+∞)时，f(x)有反函数，所以③正确；

对于④应有⇒a＞－3，

所以④错误，综上所述，只有②③正确．

15．函数f(x)＝+2的最小值为________．

答案：1+2

解析：由得x≤0或x≥4.

当x≥4时，f(x)为增函数．当x≤0时，f(x)为减函数．又∵f(0)＝2²＝4，f(4)＝2+1，∴f(x)_min＝f(4)＝1+2.

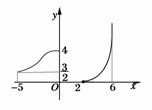
14．函数y＝f(x)的图象如右图所示，命题：

①函数f(x)的定义域是[－5,6]；

②函数f(x)的值域是[0，+∞)；

③函数f(x)在定义域内是增函数；

④函数y＝f(x)有反函数．

其中正确命题的序号是__________．

答案：②

解析：由图可知f(x)的定义域为[－5,0]∪[2,6]，

∴①错．

f(x)值域为[0，+∞)，∴②正确．

f(x)在[－5,0]和[2,6]上是增函数，但在定义域内不是增函数，

∴③错，由于y在[，4]内取一个值时，x有两个值与之对应，

∴y＝f(x)无反函数，故④错．

13．(2009·乌鲁木齐市模拟)函数y＝ln(1+x)(1－x)的单调增区间是________．

答案：(－1,0)

解析：本题考查复合函数单调区间的确定；据题意需(1+x)(1－x)＞0即函数定义域为(－1,1)，原函数的递增区间即为函数u(x)＝(1+x)(1－x)在(－1,1)上的递增区间，由于u′(x)＝－2x＞0.故函数u(x)＝在(－1,0)上的递增区间即为原函数的递增区间．

12．(2009·成都市高中毕业班第一次诊断性检测题)已知函数f(x)＝，设f₁(x)＝f(x)，f_n+1(x)＝f[f_n(x)](n∈N^*)，若集合M＝{x∈R|f₂₀₀₉(x)＝2x+}，则集合M中的元素个数为(　)

A．0个　 　　　　　　　　　　　　　 B．1个

C．2个　 　　　　　　　　　　　　　 D．无穷多个

答案：B

解析：依题意得f₁(x)＝，f₂(x)＝，f₃(x)＝x，f₄(x)＝f₁(x)，…，即函数列{f_n(x)}是以3为周期的函数列，注意到2009＝3×669+2，因此f₂₀₀₉(x)＝f₂(x)＝.

由＝2x+得2x(x+1)＝0，又x+1≠0，因此x＝0，集合M中的元素个数是1，选B.

第Ⅱ卷(非选择题　共90分)