
题目列表(包括答案和解析)
9、已知函数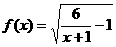 的定义域为集合A,函数
的定义域为集合A,函数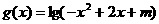 的定义域为集合B
的定义域为集合B
(1)当m=3时,求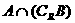 ; (2)若
; (2)若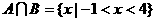 ,求实数m的值。
,求实数m的值。
8、设实数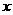 满足
满足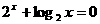 ,则
,则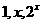 的大小关系为
的大小关系为
7、已知 (
(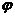 为锐角且为常数)在
为锐角且为常数)在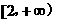 上为减函数,则实数
上为减函数,则实数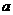 的取值范围为_________________
的取值范围为_________________
6、已知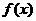
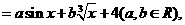 且
且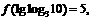 则
则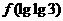 =__________.
=__________.
5、函数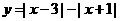 的单调递减区间是___________
的单调递减区间是___________
4、要使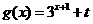 的图象不经过第二象限,则t的取值范围为
的图象不经过第二象限,则t的取值范围为
3、若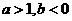 ,且
,且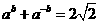 ,则
,则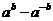 的值为
的值为
2、在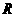 上定义的函数
上定义的函数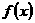 是偶函数,且
是偶函数,且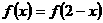 ,若
,若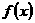 在区间
在区间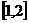 是减函数,则函数
是减函数,则函数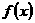 在区间
在区间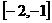 上是
函数,区间
上是
函数,区间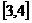 上是
函数.(填“增”或“减”)
上是
函数.(填“增”或“减”)
1、函数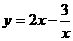 在
在 上的值域为
上的值域为
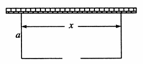
22. (2009·湖北,17)(本小题满分12分)围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽度为2m的进出口,如图所示.已知旧墙的维修费用为45元/m,新墙的造价为180元/m.设利用的旧墙长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元).
(2009·湖北,17)(本小题满分12分)围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽度为2m的进出口,如图所示.已知旧墙的维修费用为45元/m,新墙的造价为180元/m.设利用的旧墙长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元).
(1)将y表示为x的函数;
(2)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
 分析:本小题主要考查函数和不等式等基础知识,考查用平均不等式求最值和运用数学知识解决实际问题的能力.
分析:本小题主要考查函数和不等式等基础知识,考查用平均不等式求最值和运用数学知识解决实际问题的能力.
解析:(1)如图,设矩形的另一边长为am,
则y=45x+180(x-2)+180·2a=255x+360a-360.
由已知xa=360,得a=,
∴y=255x+-360(x>0).
(2)∵x>0,∴225x+≥2=10800.
∴y=225x+-360≥10440.
当且仅当225x=时,等号成立.
即当x=24m时,修建围墙的总费用最小,
最小总费用是10440元.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com