
题目列表(包括答案和解析)
5.(2009·郑州二模)设向量i、j为直角坐标系的x轴、y轴正方向上的单位向量,若向量a=(x+1)i+yj,b=(x-1)i+yj,且|a|-|b|=1,则满足上述条件的点P(x,y)的轨迹方程是 ( )
A.-=1(y≥0) B.-=1(x≥0)
C.-=1(y≥0) D.-=1(x≥0)
答案:B
解析:a=(x+1)i+yj,b=(x-1)i+yj,|a|-|b|=-=1,满足上述条件的点P(x,y)的轨迹是以(-1,0)和(1,0)为焦点的双曲线的右支,方程是-=1(x≥0),故选B.
4.(2009·石家庄市高中毕业班复习教学质量检测)从抛物线y2=4x上一点P引其准线的垂线,垂足为M,设抛物线的焦点为F,且|PF|=5,则△MPF的面积为 ( )
A.5 B. C.20 D.10
答案:D
解析:由题意,设P(,y0),则|PF|=|PM|=+1=5,所以y0=±4,S△MPF=|PM||y0|=10.
3.抛物线y2=4x,经过点P(3,m),则点P到抛物线焦点的距离等于 ( )
A. B.4 C. D.3
答案:B
解析:y2=4x的准线方程为x=-1,则点P到它的距离为3+1=4,故选B.
2.下列双曲线中,以y=±x为渐近线的是 ( )
A.-=1 B.-=1
C.-y2=1 D.x2-=1
答案:A
解析:由y=±x得±=0,因此以±=0为渐近线的双曲线为-=m(m≠0)
当m=4时,方程为-=1,故选A.
1.双曲线mx2+y2=1的虚轴长是实轴长的2倍,则m等于 ( )
A.- B.-4 C.4 D.
答案:A
命题意图:主要考查双曲线的标准形式及相关的概念,考查学生转化及计算的能力.
解析:双曲线方程化为标准形式:y2-=1则有:a2=1,b2=-,
∴2a=2,2b=2,∴2×2=2,∴m=-.
总结评述:双曲线作为圆锥曲线的一种,其几何性质常作为高考命题的热点问题,但难度一般不大,掌握其实轴、虚轴、焦距之间的关系和准线、渐近线方程是解决双曲线问题的突破口.
10.中心在坐标原点,焦点 和
和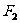 在坐标轴上,离心率为
在坐标轴上,离心率为 ,双曲线C过点P
,双曲线C过点P ,求:(1)曲线C的方程;
,求:(1)曲线C的方程;
(2)若点M(3,m)在C上,求证:
(3)求 的面积S .
的面积S .
*11.已知椭圆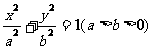 的两个焦点分别是
的两个焦点分别是 和
和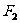 ,斜率为k的直线L过右焦点
,斜率为k的直线L过右焦点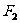 ,且与椭圆交于A、B两点,与y轴交于C点,且B为线段C
,且与椭圆交于A、B两点,与y轴交于C点,且B为线段C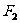 的中点
的中点
(1)若 ,求椭圆离心率的取值范围
,求椭圆离心率的取值范围
(2)若 ,且A、B到椭圆右准线的距离之和为
,且A、B到椭圆右准线的距离之和为 ,试确定椭圆的方程
,试确定椭圆的方程
9.在面积为1的△ ,
, ,
, ,建立适当的坐标系,求出以
,建立适当的坐标系,求出以 、
、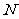 为焦点且过
为焦点且过 点的椭圆的方程.
点的椭圆的方程.
7. 、
、 是椭圆的两个焦点,
是椭圆的两个焦点, 是椭圆上的任一点,从任一焦点向△
是椭圆上的任一点,从任一焦点向△ 的顶角
的顶角 的外角平分线作垂线,垂足为
的外角平分线作垂线,垂足为 ,点
,点 的轨迹是曲线
的轨迹是曲线 的一部分,则曲线
的一部分,则曲线 是 ___________
是 ___________
(选填 圆 , 椭圆, 双曲线 , 抛物线)
*8.设P为 上一点,
上一点, 和
和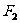 为焦点,则
为焦点,则 的最小值为________
的最小值为________
6.以曲线y 上的任意一点为圆心作圆与直线x+2=0相切,则这些圆必过一定点,则这一定点的坐标是_________.
上的任意一点为圆心作圆与直线x+2=0相切,则这些圆必过一定点,则这一定点的坐标是_________.
5.双曲线 的离心率为2, 有一个焦点与抛物线
的离心率为2, 有一个焦点与抛物线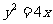 的焦点重合,则mn的值为________.
的焦点重合,则mn的值为________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com