4、已知复数z₁=cosθ-i，z₂=sinθ+i，则z₁·z₂的实部的最大值为　　　　 ，虚部最大值

为　　　　 　　　　

3、已知复数z₁=1-i，z₁·z₂=1+i，则复数z₂=　　 ____　 　

2、设复数z₁=1+i，z₂=x+2i(x∈R)。若z₁·z₂为实数，则x=　 ____　

1、=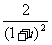　　　　

28．(本小题满分10分)已知z₁＝a+(a+1)i，z₂＝－3b+(b+2)i(a＞0、b＞0)且3z+z＝0，求z₁和z₂.

解析：∵3z+z＝0，

∴()²＝－3，即＝±i.

∴z₂＝±iz₁.

当z₂＝iz₁时，得

－3b+(b+2)i＝i[a+(a+1)i]＝－(a+1)+ai.

由复数相等的条件，知

∴

∴z₁＝+3i，z₂＝－3+3i.

当z₂＝－iz₁时，得－3b+(b+2)i＝(a+1)－ai，

由复数相等的条件，知

∴

∵已知a，b∈(0，+∞)，

∴此时适合条件的a，b不存在．

∴z₁＝+3i，z₂＝－3+3i.

27．(本小题满分10分)求同时满足下列两个条件的所有复数z；

(1)1＜z+≤6；

(2)z的实部和虚部都是整数．

解析：设z＝x+yi(x，y∈R)，

则z+＝+i.

∵1＜z+≤6，∴

由①得y＝0或x²+y²＝10，将y＝0代入②得1＜+x≤6，与+x≥2＞6(x＞0)矛盾，

∴y≠0.将x²+y²＝10代入②得＜x≤3.

又x，y为整数，∴或

故z＝1±3i或z＝3±i.

26．(本小题满分10分)计算下列问题：

(1)+－；

(2)(－－i)¹²+()⁸.

分析：对于复数运算，除了应用四则运算法则之外，对于一些简单算式是知道其结果，这样起点高，方便计算，达到迅速简捷、少出错的效果．比如(1±i)²＝±2i，＝－i，＝i，＝－i，＝b－ai，(－±i)³＝1，(±i)³＝－1等等．

解析：(1)原式＝[(1+i)²]³·+[(1－i)²]³·－＝(2i)³·i+(－2i)³·(－i)－

＝8+8－16－16i＝－16i.

(2)(－－i)¹²+()⁸

＝i¹²·(－+i)¹²+⁸

＝[(－+i)³]⁴+

＝1－(2i)⁴(－i)

＝1－8+8i＝－7+8i.

25．(2009·安徽宿州二中模拟考三)i是虚数单位，则1+Ci+Ci²+Ci³+Ci⁴+Ci⁵+Ci⁶＝________.

答案：－8i

解析：1+Ci+Ci²+Ci³+Ci⁴+Ci⁵+Ci⁶＝(1+i)⁶＝[(1+i)²]³＝(2i)³＝－8i.

24．(2009·海淀4月)在复平面内，复数(a∈R)对应的点位于虚轴上，则a＝________.

答案：0

解析：＝a－i，由于它对应的点在虚轴上，则a＝0.

23．(2009·江苏)若复数z₁＝4+29i，z₂＝6+9i，其中i是虚数单位，则复数(z₁－z₂)i的实部为________．

答案：－20

解析：(z₁－z₂)i＝(－2+20i)i＝－20－2i，故(z₁－z₂)i的实部为－20.