
题目列表(包括答案和解析)
18.(1)证法1:∵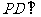 平面
平面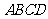 ,
,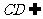 平面
平面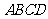 ,∴
,∴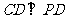 .
.
又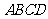 为正方形,∴
为正方形,∴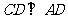 .∵
.∵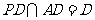 ,∴
,∴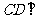 平面
平面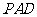 .
.
∵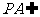 平面
平面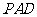 ,∴
,∴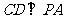 .∵
.∵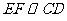 ,∴
,∴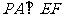 .
.
证法2:以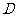 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系 ,
,
则 ,
,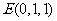 ,
,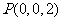 ,
,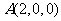 ,
, ,
,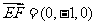 .
.
 ∵
∵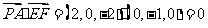 ,∴
,∴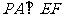 .
.
(2)解法1:以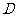 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系 ,
,
则 ,
, ,
,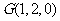 ,
,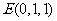 ,
,
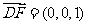 ,
,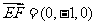 ,
,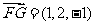 .
.
设平面DFG的法向量为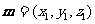 ,∵
,∵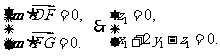
令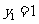 ,得
,得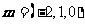 是平面
是平面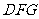 的一个法向量.
的一个法向量.
设平面EFG的法向量为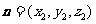 ,∵
,∵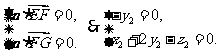
令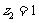 ,得
,得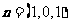 是平面
是平面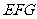 的一个法向量.
的一个法向量.
∵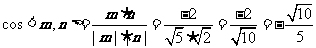 .
.
设二面角 的平面角为θ,则
的平面角为θ,则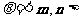 .
.
所以二面角 的余弦值为
的余弦值为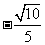 .
.
解法2:以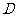 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系 ,
,
则 ,
, ,
,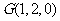 ,
,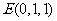 ,
,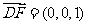 ,
,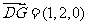 ,
,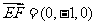 ,
,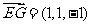 ,
,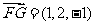 .………………………………8分
.………………………………8分
 过
过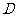 作
作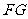 的垂线,垂足为
的垂线,垂足为 ,
,
∵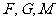 三点共线,∴
三点共线,∴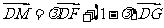 ,
,
∵ ,∴
,∴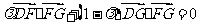 ,
,
即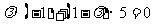 ,解得
,解得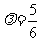 .
.
∴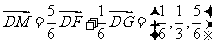 .…………10分
.…………10分
再过 作
作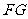 的垂线,垂足为
的垂线,垂足为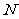 ,
,
∵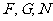 三点共线,∴
三点共线,∴ ,
,
∵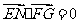 ,∴
,∴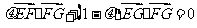 ,
,
即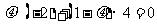 ,解得
,解得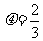 .
.
∴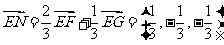 .∴
.∴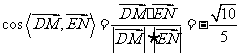 .
.
∵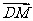 与
与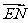 所成的角就是二面角
所成的角就是二面角 的平面角,
的平面角,
所以二面角 的余弦值为
的余弦值为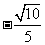 .
.
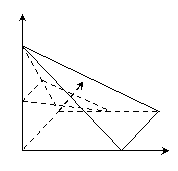
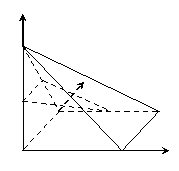
18.如图3所示,四棱锥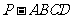 中,底面
中,底面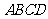 为正方形,
为正方形,
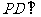 平面
平面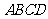 ,
,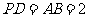 ,
, ,
,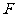 ,
,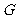 分别为
分别为
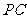 、
、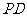 、
、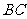 的中点.
的中点.
(1)求证: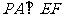 ;
;
(2)求二面角D-FG-E的余弦值.
17.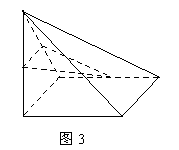 将棱长为3的正四面体以各顶点截去四个棱长为1的小正四面体(使截面平行于底面),所得几何体的表面积为
将棱长为3的正四面体以各顶点截去四个棱长为1的小正四面体(使截面平行于底面),所得几何体的表面积为 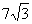 。
。
16.过椭圆的左焦点F且倾斜角为60°的直线交椭圆于A,B两点,若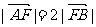 ,则椭圆的离心率e=
,则椭圆的离心率e=  。
。
15.已知函数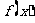 的导函数为
的导函数为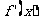 ,且满足
,且满足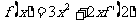 ,则
,则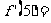 6 。
6 。
14.已知数列{an}的前n项的和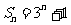 ,则数列{an}的通项an= .
,则数列{an}的通项an= . 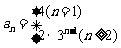
13. 在半径为R的圆内,作内接等腰三角形,当底边上高为___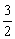 R
______时它的面积最大.
R
______时它的面积最大.
12.在三角形 ABC中,A=120°,AB=5,BC=7,则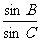 的值为___________;
的值为___________;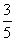
11. 若抛物线y2=2px的焦点与双曲线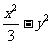 =1的右焦点重合,则实数p = 4
=1的右焦点重合,则实数p = 4
10. 在O点测量到远处有一物体在作等速直线运动, 开始时该物位于P点,一分钟后,其位置在Q点,且∠POQ = 90°, 再过一分钟后,该物体位于R点,且∠QOR =30°, 则
tan2∠OPQ 等于 A.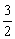 B.
B.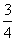 C.
C. 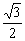 D.
D. 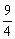 ( B )
( B )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com