
题目列表(包括答案和解析)
12.(选做)设函数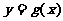 的定义域是R,且对任意的
的定义域是R,且对任意的
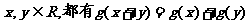 成立,又当
成立,又当 时,
时, 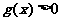 .
.
(1) 函数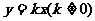 是否是上述函数的特例?若是,请说明理由;若不是,另举出一例.
是否是上述函数的特例?若是,请说明理由;若不是,另举出一例.
(2) 类比(1)是具体函数的性质,试推广出上述一般函数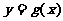 的两个性质,并给出证明.
的两个性质,并给出证明.
11.是否存在无穷等差数列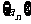 ,使它的前
,使它的前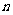 项的和
项的和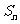 满足对任意的正整数
满足对任意的正整数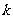 ,都有
,都有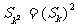 ,说明理由.
,说明理由.
10.已知 .通过观察上述两个等式的规律,请写出一个一般性的命题,并给出证明.
.通过观察上述两个等式的规律,请写出一个一般性的命题,并给出证明.
9.(选做)设函数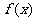 的定义域为
的定义域为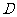 ,若存在一个正数
,若存在一个正数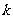 ,满足:对任意的
,满足:对任意的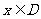 ,都有
,都有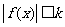 ,则称函数
,则称函数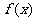 在
在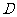 上是“有界函数”.已知下列函数:①
上是“有界函数”.已知下列函数:① ;②
;②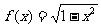 ;③
;③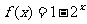 ;④
;④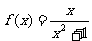 .其中是“有界函数”的是____________.(写出所有满足要求的函数序号)
.其中是“有界函数”的是____________.(写出所有满足要求的函数序号)
8.已知数列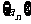 的前
的前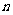 项和为
项和为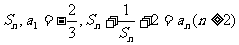 ,依次计算
,依次计算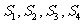 后,猜想
后,猜想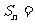 _______________.
_______________.
7.如果一个凸多面体是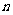 棱锥,那么这个凸多面体的所有顶点所确定的直线共有________条.这些直线中共有
棱锥,那么这个凸多面体的所有顶点所确定的直线共有________条.这些直线中共有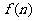 对异面直线,则
对异面直线,则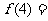 _________;
_________;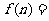 _________.(答案用数字或的解析式表示)
_________.(答案用数字或的解析式表示)
6.已知函数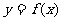 ,对于任意两个实数
,对于任意两个实数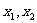 ,有
,有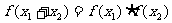 且
且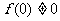 则
则 _____.
_____.
5.在数列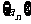 中,
中,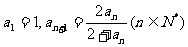 .猜想这个数列的通项公式
.猜想这个数列的通项公式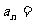 ____________.
____________.
4.已知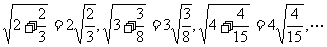 ,若
,若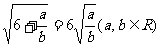 ,试推测
,试推测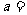 _________,
_________,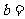 ________.
________.
3.平面几何中“周长一定的所有矩形中,正方形的面积最大.”类比到空间可得到结论_____________________________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com