
题目列表(包括答案和解析)
2.
 三类角的定义及求法
三类角的定义及求法
(1)异面直线所成的角θ,0°<θ≤90°
(2)直线与平面所成的角θ,0°≤θ≤90°
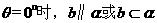
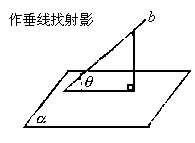
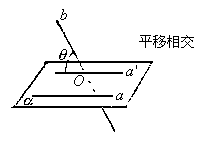
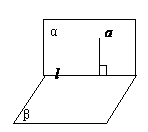
(3)二面角:二面角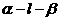 的平面角
的平面角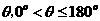
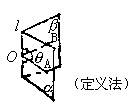
 三垂线定理法:A∈α作或证AB⊥β于B,作BO⊥棱于O,连AO,则AO⊥棱l,∴∠AOB为所求。
三垂线定理法:A∈α作或证AB⊥β于B,作BO⊥棱于O,连AO,则AO⊥棱l,∴∠AOB为所求。
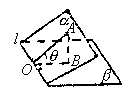
三类角的求法:
①找出或作出有关的角。
 ②证明其符合定义,并指出所求作的角。
②证明其符合定义,并指出所求作的角。
③计算大小(解直角三角形,或用余弦定理)。
[练习]
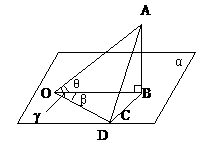
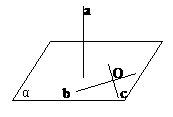
(1)如图,OA为α的斜线OB为其在α内射影,OC为α内过O点任一直线。证明: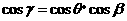
 为线面成角,
为线面成角,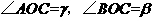
(2)如图,正四棱柱ABCD-A1B1C1D1中对角线BD1=8,BD1与侧面B1BCC1所成的为30°。
①求BD1和底面ABCD所成的角;
②求异面直线BD1和AD所成的角;
③求二面角C1-BD1-B1的大小。
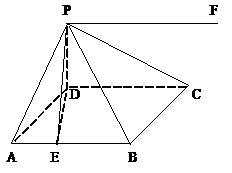
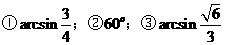
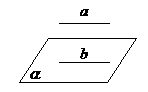
(3)如图ABCD为菱形,∠DAB=60°,PD⊥面ABCD,且PD=AD,求面PAB与面PCD所成的锐二面角的大小。
∵AB∥DC,P为面PAB与面PCD的公共点,作PF∥AB,则PF为面PCD与面PAB的交线……
1.平行、垂直关系证明的思路
平行垂直的证明主要利用线面关系的转化:
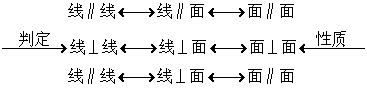 线面平行的判定:
线面平行的判定: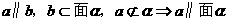
线面平行的性质: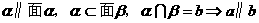
三垂线定理(及逆定理):
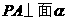 ,
, 为
为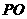 在
在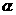 内射影,
内射影,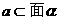 ,则
,则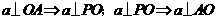
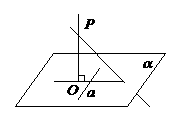 线面垂直:
线面垂直:
面面垂直: ,
,
10. 常用函数的图象和性质
常用函数的图象和性质
(1)
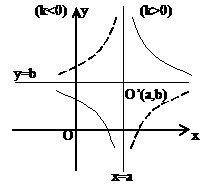
 (2)反比例函数:
(2)反比例函数: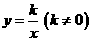 推广为
推广为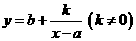 是中心
是中心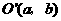 的双曲线。
的双曲线。
(3)二次函数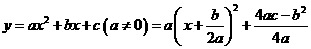 的图像为抛物线
的图像为抛物线
顶点坐标为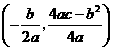 ,对称轴
,对称轴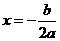
开口方向: ,向上,函数
,向上,函数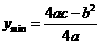
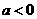 ,向下,
,向下,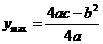
应用:①“三个二次”(二次函数、二次方程、二次不等式)的关系--二次方程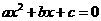 ,
,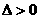 时,两根
时,两根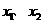 为二次函数
为二次函数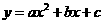 的图像与
的图像与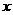 轴的两个交点,也是二次不等式
轴的两个交点,也是二次不等式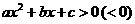 解集的端点值。
解集的端点值。
②求闭区间[m,n]上的最值。
③求区间定(动),对称轴动(定)的最值问题。
④一元二次方程根的分布问题。
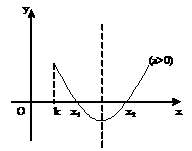
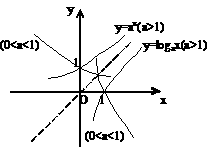 如:二次方程
如:二次方程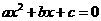 的两根都大于
的两根都大于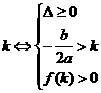 ,一根大于
,一根大于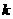 ,一根小于
,一根小于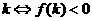
(4)指数函数: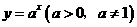
(5)对数函数: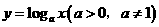
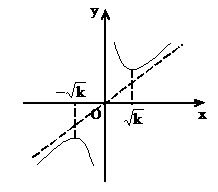 由图象记性质!(注意底数的限定!)
由图象记性质!(注意底数的限定!)
(6)“对勾函数”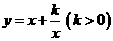
利用它的单调性求最值与利用均值不等式求最值的区别是什么?
必修二 一、 立体几何
9. 函数图象⑴图象作法 :①描点法(注意三角函数的五点作图)②图象变换法③导数法
⑵图象变换:
① 平移变换:ⅰ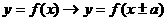 ,
,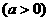 ---左“+”右“-”;
---左“+”右“-”;
ⅱ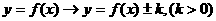 ---上“+”下“-”;
---上“+”下“-”;
② 伸缩变换:
ⅰ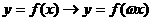 , (
, (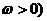 ---纵坐标不变,横坐标伸长为原来的
---纵坐标不变,横坐标伸长为原来的 倍;
倍;
ⅱ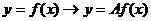 , (
, (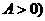 ---横坐标不变,纵坐标伸长为原来的
---横坐标不变,纵坐标伸长为原来的 倍;
倍;
③ 对称变换:ⅰ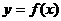
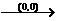
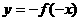 ;ⅱ
;ⅱ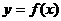
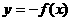 ;
;
ⅲ 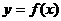
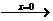
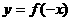 ; ⅳ
; ⅳ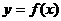
 ;
;
④ 翻转变换:
ⅰ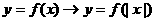 ---右不动,右向左翻(
---右不动,右向左翻(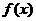 在
在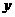 左侧图象去掉);
左侧图象去掉);
ⅱ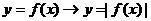 ---上不动,下向上翻(|
---上不动,下向上翻(|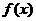 |在
|在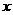 下面无图象);
下面无图象);
8.函数的单调性。
如何用定义证明函数的单调性?(取值、作差、判正负)
如何判断复合函数的单调性?
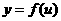 (外层),
(外层),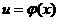 (内层),则
(内层),则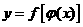
当内、外层函数单调性相同时,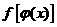 为增函数,否则
为增函数,否则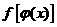 为减函数
为减函数
如:求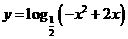 的单调区间。
的单调区间。
设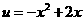 ,由
,由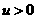 ,则
,则 且
且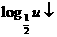 ,
, ,如图
,如图
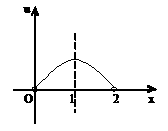 当
当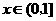 时,
时,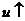 ,又
,又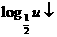 ,∴
,∴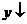
当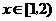 时,
时,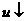 ,又
,又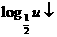 ,∴
,∴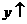
∴……)
7. 函数的奇偶性⑴函数的定义域关于原点对称是函数具有奇偶性的必要条件;
⑵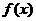 是奇函数
是奇函数
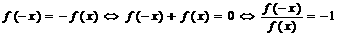 ;
;
⑶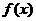 是偶函数
是偶函数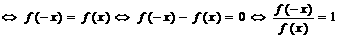 ;
;
⑷奇函数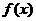 在原点有定义,则
在原点有定义,则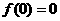 ;
;
⑸在关于原点对称的单调区间内:奇函数有相同的单调性,偶函数有相反的单调性;
(6)若所给函数的解析式较为复杂,应先等价变形,再判断其奇偶性;
6.求函数解析式的常用方法:
(1)待定系数法―已知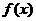 为二次函数,且
为二次函数,且 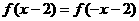 ,且f(0)=1,图象在x轴上截得的线段长为2
,且f(0)=1,图象在x轴上截得的线段长为2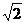 ,求
,求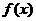 的解析式 。(答:
的解析式 。(答: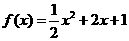 )
)
(2)配凑法―①已知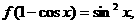 求
求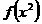 的解析式___(答:
的解析式___(答: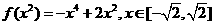 );②若
);②若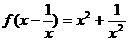 ,则函数
,则函数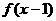 =___(答:
=___(答: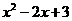 );
);
(3)方程的思想―已知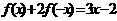 ,求
,求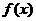 的解析式(答:
的解析式(答: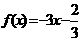 );
);
5.分段函数的概念。(1)设函数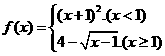 ,则使得
,则使得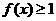 的自变量
的自变量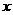 的取值范围是____(答:
的取值范围是____(答: );(2)已知
);(2)已知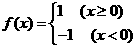 ,则不等式
,则不等式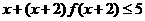 的解集是___(答:
的解集是___(答: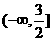 )
)
4.求函数值域(最值)的方法:
(1)配方法―①当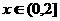 时,函数
时,函数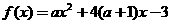 在
在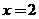 时取得最大值,则
时取得最大值,则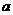 的取值范围是___(答:
的取值范围是___(答: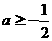 );
);
(2)换元法①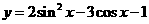 的值域为_____(答:
的值域为_____(答: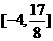 );②
);②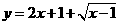 的值域为_____(答:
的值域为_____(答: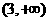 )(令
)(令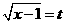 ,
,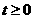 。运用换元法时,要特别要注意新元
。运用换元法时,要特别要注意新元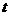 的范围);3
的范围);3 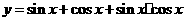 的值域为____(答:
的值域为____(答: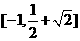 );4
);4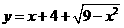 的值域为____(答:
的值域为____(答: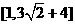 );
);
(3)函数有界性法―求函数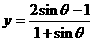 ,
,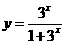 ,
,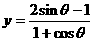 的值域(答:
的值域(答: 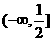 、(0,1)、
、(0,1)、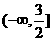 );
);
(4)单调性法――求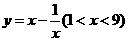 ,
,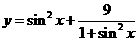 的值域为______(答:
的值域为______(答: 、
、 );
);
(5)数形结合法――已知点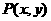 在圆
在圆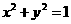 上,求
上,求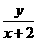 及
及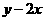 的取值范围(答:
的取值范围(答: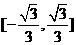 、
、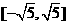 );
);
(6)不等式法―设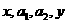 成等差数列,
成等差数列,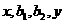 成等比数列,则
成等比数列,则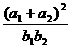 的取值范围是____________.(答:
的取值范围是____________.(答: )。
)。
3.研究函数问题时要树立定义域优先的原则:
(1)函数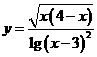 的定义域是____(答:
的定义域是____(答: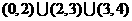 );
);
(2)设函数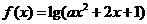 ,①若
,①若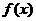 的定义域是R,求实数
的定义域是R,求实数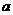 的取值范围;②若
的取值范围;②若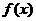 的值域是R,求实数
的值域是R,求实数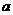 的取值范围(答:①
的取值范围(答:①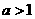 ;②
;②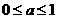 )
)
(3)复合函数的定义域:①若函数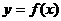 的定义域为
的定义域为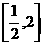 ,则
,则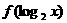 的定义域为__________(答:
的定义域为__________(答: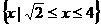 );②若函数
);②若函数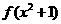 的定义域为
的定义域为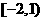 ,则函数
,则函数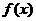 的定义域为________(答:[1,5]).
的定义域为________(答:[1,5]).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com