14．点P(a,3)到直线4x－3y+1＝0的距离等于4，且在不等式2x+y＜4表示的平面区域内，则P点的坐标为__________．

答案：(－3,3)

解析：因＝4，∴a＝7，a＝－3.

当a＝7时，不满足2x+y＜4(舍去)，∴a＝－3.

13．(2010·湖南长沙一中)已知直线l₁：ax+y+2a＝0，直线l₂：ax－y+3a＝0.若l₁⊥l₂，则a＝________.

答案：±1

解析：∵l₁⊥l₂，∴kl₁·kl₂＝－1，即(－a)·a＝－1，∴a＝±1.

12．(2010·保定市高三摸底考试)从原点向圆x²+(y－6)²＝4作两条切线，则这两条切线夹角的大小为　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.　 　　　　　　 B.　　　 C．arccos　 　　　　　　　 D．arcsin

答案：C

解析：如图，sin∠AOB＝＝，cos∠BOC＝cos2∠AOB＝1－2sin²∠AOB＝1－＝，∴∠BOC＝arccos，故选C.

第Ⅱ卷(非选择题　共90分)

11．(2009·河南实验中学3月)若直线l：ax+by＝1与圆C：x²+y²＝1有两个不同交点，则点P(a，b)与圆C的位置关系是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．点在圆上　 　　　　　　 B．点在圆内　　 C．点在圆外　 　　　 D．不能确定

答案：C

解析：直线l：ax+by＝1与圆C：x²+y²＝1有两个不同交点，则＜1，a²+b²＞1，点P(a，b)在圆C外部，故选C.

10．(2009·安阳，6)已知直线x+y＝a与圆x²+y²＝4交于A、B两点，且|+|＝|－|，其中O为原点，则实数a的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．2　 　　　　　　　　 B．－2 　　　　C．2或－2　 　　　　　 　　D.或－

答案：C

解析：由|+|＝|－|得|+|²＝|－|²，·＝0，⊥，三角形AOB为等腰直角三角形，圆心到直线的距离为，即＝，a＝±2，故选C.

9．(2009·西城4月，6)与直线x－y－4＝0和圆x²+y²+2x－2y＝0都相切的半径最小的圆的方程是　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．(x+1)²+(y+1)²＝2　 　　　　　 B．(x+1)²+(y+1)²＝4

C．(x－1)²+(y+1)²＝2　 　　　　　 D．(x－1)²+(y+1)＝4

答案：C

解析：圆x²+y²+2x－2y＝0的圆心为(－1,1)，半径为，过圆心(－1,1)与直线x－y－4＝0垂直的直线方程为x+y＝0，所求的圆的圆心在此直线上，排除A、B，圆心(－1,1)到直线x－y－4＝0的距离为＝3，则所求的圆的半径为，故选C.

8．(2009·陕西，4)过原点且倾斜角为60°的直线被圆x²+y²－4y＝0所截得的弦长为

(　)

A.　 　　　　　　　　 B．2 　　　　　　　　　　　　 C.　 　　　　　　　　　　　　 D．2

答案：D

解析：∵直线的方程为y＝x，圆心为(0,2)，半径r＝2.

由点到直线的距离公式得弦心距等于1，从而所求弦长等于2＝2.故选D.

7．(2009·福建，9)在平面直角坐标系中，若不等式组(a为常数)所表示的平面区域的面积等于2，则a的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．－5　 　　　　　　 B．1 　　　　　　　　　　　　 C．2　 　　　　　　　　　　　　 D．3

答案：D

解析：不等式组所围成的区域如图所示．

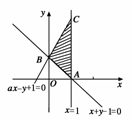
∵其面积为2，∴|AC|＝4，

∴C的坐标为(1,4)，代入ax－y+1＝0，

得a＝3.故选D.

6．两直线2x－my+4＝0和2mx+3y－6＝0的交点在第二象限，则m的取值范围是

(　)

A．－≤m≤2　 　　　　　　　　　　　 B．－＜m＜2

C．－≤m＜2　 　　　　　　　　　　　 D．－＜m≤2

答案：B

解析：由解得两直线的交点坐标为(，)，由交点在第二象限知横坐标为负、纵坐标为正，故＜0且＞0⇒－＜m＜2.

5．直线x+a²y+6＝0和(a－2)x+3ay+2a＝0无公共点，则a的值是　　　　 (　)

A．3　 　　　　　　　　 B．0 　　　　　　　　　　　　 C．－1　 　　　　　　　　　　 D．0或－1

答案：D

解析：当a＝0时，两直线方程分别为x+6＝0和x＝0，显然无公共点；当a≠0时，－＝－，∴a＝－1或a＝3.而当a＝3时，两直线重合，∴a＝0或－1.