
题目列表(包括答案和解析)
1、设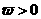 ,若函数
,若函数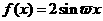 在
在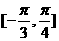 上单调递增,则
上单调递增,则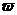 的取值范围是_______
的取值范围是_______
22.(2009·河南郑州模拟)(本小题满分12分)已知A、B、C三点的坐标分别是A(3,0)、B(0,3),C(cosα,sinα),其中<α<.
(1)若||=||,求角α的值;
(2)若·=-1,求的值.
解析:(1)=(cosα-3,sinα),=(cosα,sinα-3),
∵||=||,∴||2=||2,
即(cosα-3)2+sin2α=cos2α+(sinα-3)2,
化简得sinα=cosα.
∵<α<,∴α=.
(2)-1=·=cosα(cosα-3)+sinα(sinα-3)=1-3(sinα+cosα),
∴sinα+cosα=.
于是2sinα·cosα=(sinα+cosα)2-1=-,
故==2sinα·cosα=-.
21.(本小题满分12分)已知tanα、tanβ是方程x2-4x-2=0的两个实根,求:cos2(α+β)+2sin(α+β)cos(α+β)-3sin2(α+β)的值.
解析:由已知有tanα+tanβ=4,
tanα·tanβ=-2,
∴tan(α+β)==,
cos2(α+β)+2sin(α+β)cos(α+β)-3sin2(α+β)
=
=
==-.
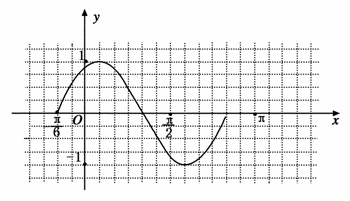
20.(2009·大同模拟)(本小题满分12分)已知函数f(x)=2cosx·sin(x+)-.
(1)求函数f(x)的最小正周期T;
(2)在给定的坐标系中,用“五点法”作出函数f(x)在一个周期上的函数.
解析:(1)f(x)=2cosx·sin(x+)-
=2cosx(sinxcos+cosxsin)-
=2cosx(sinx+cosx)-
=sinxcosx+·cos2x-
=sin2x+·-
=sin2x+cos2x
=sin(2x+).
∴T===π.
即函数f(x)的最小正周期为π.
(2)列表:
|
x |
- |
|
|
|
|
|
2x+ |
0 |
|
π |
π |
2π |
|
sin(2x+) |
0 |
1 |
0 |
-1 |
0 |
描点画图:
19.(2009·福州质检)(本小题满分12分)已知f(x)=sin2wx+sin2wx-(x∈R,w>0),若f(x)的最小正周期为2π.
(1)求f(x)的表达式和f(x)的单调递增区间;
(2)求f(x)在区间[-,]上的最大值和最小值.
解析:(1)由已知f(x)=sin2wx+sin2wx-=(1-cos2wx)+sin2wx-=sin2wx-cos2wx=sin(2wx-).
又由f(x)的周期为2π,则2π=⇒2w=1⇒w=,
⇒f(x)=sin(x-),
2kπ-≤x-≤2kπ+(k∈Z)⇒2kπ-≤x≤2kπ+(k∈Z),
即f(x)的单调递增区间为
[2kπ-,2kπ+](k∈Z).
(2)由x∈[-,]⇒-≤x≤⇒--≤x-≤-⇒-≤x-≤⇒sin(-)≤sin(x-)≤sin.∴-≤sin(x-)≤1.
故f(x)在区间[-,]的最大值和最小值分别为1和-.
18.(2009·浙江金华)(本小题满分12分)已知函数f(x)=Asin(wx+φ),(A>0,w>0,|φ|<,x∈R)的图象的一部分如图所示.
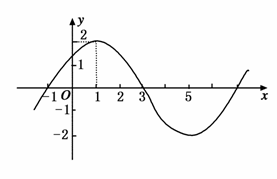
(1)求函数f(x)的解析式;
(2)当x∈[-6,]时,求函数y=f(x)+f(x+2)的最大值与最小值及相应的x的值.
解析:(1)由图象知A=2,T=8,
∵T==8,∴w=.
又∵图象经过点(-1,0),
∴2sin(-+φ)=0.
∵|φ|<,∴φ=,
∴f(x)=2sin(x+).
(2)y=f(x)+f(x+2)
=2sin(x+)+2sin(x++)
=2sin(x+)
=2cosx,
∵x∈[-6,],∴-≤x≤.
∴当x=0,即x=0时,
y=f(x)+f(x+2)的最大值为2,
当x=-π,即x=-4时,最小值为-2.
17.(本小题满分10分)已知α∈(0,),β∈(,π)且sin(α+β)=,cosβ=-.求sinα.
解析:∵β∈(,π),cosβ=-,∴sinβ=.
又∵0<α<,<β<π,
∴<α+β<,又sin(α+β)=,
∴<α+β<π,
cos(α+β)=-
=-=-,
∴sinα=sin[(α+β)-β]
=sin(α+β)cosβ-cos(α+β)sinβ
=·(-)-(-)·=.
16.给出下列六个命题,其中正确的命题是__________.
①存在α满足sinα+cosα=;
②y=sin(π-2x)是偶函数;
③x=是y=sin(2x+)的一条对称轴;
④y=esin2x是以π为周期的(0,)上的增函数;
⑤若α、β是第一象限角,且α>β,则tanα>tanβ;
⑥函数y=3sin(2x+)的图象可由y=3sin2x的图象向左平移个单位得到.
答案:②③
解析:①sinα+cosα=sin(α+)∈[-,],
∴sinα+cosα≠.
②y=sin(-2x)=sin(-2x)=cos2x,是偶函数.
③对y=sin(2x+),由2x+=+kπ,得x=-+,(k∈Z)是对称轴方程.取k=1得x=.
④y=sin2x在(0,)上不是增函数,∴y=esin2x在(0,)上也不是增函数.
⑤y=tanx在第一象限不是增函数.∴α>β,不一定有tanα>tanβ.
⑥y=3sin(2x+)=3sin2(x+),可由y=3sin2x的图象向左平移个单位得到.
15.下图是函数y=sin(wx+φ)(w>0,|φ|<)的图象的一部分,则φ=________,w=________.
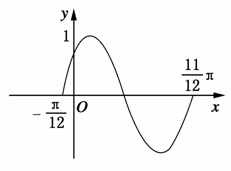
答案: 2
解析:由图知T=π-(-)=π,
∴w===2,∴y=sin(2x+φ).
又点(-,0)在图象上,∴sin(-+φ)=0,
∴-+φ=0,φ=.
14.(2009·南昌市高三年级第一次调研测试)已知sin(α+)=,则cos(α+)的值等于________.
答案:-
解析:由已知得cos(α+)=cos[(α+)+]=-sin(α+)=-.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com