20．(本小题满分12分)求关于x的方程ax²－(a²+a+1)x+a+1＝0至少有一个正根的充要条件．

解析：方法一：若a＝0，则方程变为－x+1＝0，x＝1满足条件，若a≠0，则方程至少有一个正根等价于

＜0或

或

⇔－1＜a＜0或a＞0.

综上：方程至少有一正根的充要条件是a＞－1.

方法二：若a＝0，则方程即为－x+1＝0，

∴x＝1满足条件；

若a≠0，∵△＝(a²+a+1)²－4a(a+1)

＝(a²+a)²+2(a²+a)+1－4a(a+1)

＝(a²+a)²－2a(a+1)+1＝(a²+a－1)²≥0，

∴方程一定有两个实根．

故而当方程没有正根时，应有

，解得a≤－1，

∴至少有一正根时应满足a＞－1且a≠0，

综上，方程有一正根的充要条件是a＞－1.

19．(本小题满分12分)设全集I＝R，A＝{x|x²－2x＞0，x∈R}，B＝{x|x²－ax+b＜0，x∈R}，C＝{x|x³+x²+x＝0，x∈R}．又∁_R(A∪B)＝C，A∩B＝{x|2＜x＜4，x∈R}，试求a、b的值．

解析：∵A＝{x|x＜0或x＞2}，B＝{x|x²－ax+b＜0，x∈R}＝{x|x₁＜x＜x₂，x₁、x₂∈R}，C＝{x|x＝0}，∁_R(A∪B)＝C＝{0}，

∴A∪B＝{x|x≠0且x∈R}．

又A∩B＝{x|2＜x＜4，x∈R}，可得x₁＝0，x₂＝4.

又x₁、x₂是方程x²－ax+b＝0的两根，

∴x₁+x₂＝a，x₁x₂＝b.

从而求得a＝4，b＝0.

18．(2009·山东济南高三12月月考)(本小题满分12分)已知p：方程x²+mx+1＝0有两个不相等的负实根；q：不等式4x²+4(m－2)x+1＞0的解集为R，若p或q为真命题，p且q为假命题，求m的取值范围．

解析：p为真命题⇔⇒m＞2.

q为真命题⇔△＝[4(m－2)]²－4×4×1＜0⇒1＜m＜3.

∵p或q为真，p且q为假，∴p与q一真一假．

若p真q假，则m＞2，且m≤1或m≥3，所以m≥3.

若p假q真，则m≤2，且1＜m＜3，所以1＜m≤2.

综上所述，m的取值范围为{m|1＜m≤2，或m≥3}．

17．(本小题满分10分)设集合A＝{x|x²+ax－12＝0}，B＝{x|x²+bx+c＝0}，且A≠B，A∪B＝{－3,4}，A∩B＝{－3}，求a、b、c的值．

分析：由于集合中的元素是以方程的解的形式给出的，因此要从集合中元素的特性和交、并集的含义进行思考．

解答：∵A∩B＝{－3}，∴－3∈A且－3∈B，

将－3代入方程：x²+ax－12＝0中，得a＝－1，

从而A＝{－3,4}．

将－3代入方程x²+bx+c＝0，得3b－c＝9.

∵A∪B＝{－3,4}，∴A∪B＝A，∴B⊆A.

∵A≠B，∴B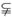A，∴B＝{－3}．

∴方程x²+bx+c＝0的判别式△＝b²－4c＝0，

∴

由①得c＝3b－9，代入②整理得：(b－6)²＝0，

∴b＝6，c＝9.

故a＝－1，b＝6，c＝9.

16．设命题p：|4x－3|≤1；命题q：x²－(2a+1)x+a(a+1)≤0.若┐p是┐q的必要而不充分条件，则实数a的取值范围是__________．

答案：[0，]

解析：解|4x－3|≤1得≤x≤1.解q得a≤x≤a+1.由题设条件得q是p的必要不充分条件，即p⇒q，q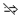p.

∴[，1]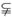[a，a+1]．

∴a≤且a+1≥1，得0≤a≤.

15．若命题p：不等式ax+b＞0的解集为{x|x＞－}，命题q：关于x的不等式(x－a)(x－b)＜0的解集为{x|a＜x＜b}，则“p且q”“p或q”及“非p”形式的复合命题中的真命题是__________．

答案：非p

解析：命题p为假命题，命题q为假命题，故只有“非p”是真命题．

14．命题“若a＞b，则2^a＞2^b－1”的否命题为______________．

答案：若a≤b，则2^a≤2^b－1

解析：写出一个命题的否命题的关键是正确找出原命题的条件和结论．

13．设集合A＝{x|(x－1)²＜3x+7，x∈R}，则集合A∩Z中有________个元素．

答案：6

解析：由(x－1)²＜3x+7可得－1＜x＜6，即得A＝(－1,6)．

∴A∩Z＝{0,1,2,3,4,5}，即得集合A∩Z中共有6个元素．

12．(2010·河南省焦作市期中试题)设集合A、B是非空集合，定义A×B＝{x|x∈A∪B且x∉A∩B}，已知A＝{x|y＝}，B＝{y|y＝2x²}，则A×B等于　　　　　　　　　　　　 (　)

A．(2，+∞)　 　　　　　　　　　　B．[0,1]∪[2，+∞)

C．[0,1)∪(2，+∞) 　　　　　　　D．[0,1]∪(2，+∞)

答案：A

解析：A＝{x|y＝}＝{x|0≤x≤2}

B＝{y|y＝2x²}＝{y|y≥0}

∴A∪B＝[0，+∞)，A∩B＝[0,2]

因此A×B＝(2，+∞)，故选A.

　　　　　　　　　　　　　　 第Ⅱ卷(非选择题　共90分)

11．(2009·湖北，5分)已知P＝{a|a＝(1,0)+m(0,1)，m∈R}，Q＝{b|b＝(1,1)+n(－1,1)，n∈R}是两个向量集合，则P∩Q＝　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．{(1,1)}　 　　　　　　　　　　　　　　　　　　 B．{(－1,1)}

C．{(1,0)}　 　　　　　　　　　　　　　　　　　　 D．{(0,1)}

答案：A

解析：由已知可求得P＝{(1，m)}，Q＝{(1－n,1+n)}，再由交集的含义，有

⇒，所以选A.