
题目列表(包括答案和解析)
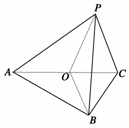
3.(2009·东北三省十校一模)三棱锥P-ABC中∠ABC=90°,PA=PB=PC,则下列说法正确的是 ( )
A.平面PAC⊥平面ABC B.平面PAB⊥平面PBC
C.PB⊥平面ABC D.BC⊥平面PAB
答案:A
解析:如图,因为∠ABC=90°,PA=PB=PC,所以点P在底面的射影落在△ABC的斜边的中点O处,连结OB、OP,则PO⊥OB.又∵PA=PC,所以PO⊥AC,且AC∩OB=O,
所以PO⊥平面ABC.
又∵PO⊂平面PAC,∴平面PAC⊥平面ABC,故选A.
2.(2009·广东重点中学)已知三条不重合的直线m、n、l与两个不重合的平面α、β,有下列命题:
①若m∥n,n⊂α,则m∥α;
②若l⊥α,m⊥β且l∥m,则α∥β;
③若m⊂α,n⊂α,m∥β,n∥β,则α∥β;
④若α⊥β,α∩β=m,n⊂β,n⊥m,则n⊥α.
其中正确的命题个数是 ( )
A.1 B.2 C.3 D.4
答案:B
解析:对于①,若m∥n,n⊂α,则m∥α或m⊂α,①不正确;对于②,若l⊥α,m⊥β且l∥m,则α∥β,显然成立;对于③,若m⊂α,n⊂α,m∥β,n∥β,则α∥β,由面面平行的判定定理知它是不正确的;对于④,若α⊥β,α∩β=m,n⊂β,n⊥m,则n⊥α,由面面垂直的性质定理知它是正确的;综上所述,正确命题的个数为2,故选B.
1.(2009·上海市普通高等学校春季招生考试)在空间中,“两条直线没有公共点”是“这两条直线平行”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
答案:B
解析:在空间中,两条直线没有公共点,这两条直线可能是异面直线,即由“两条直线没有公共点”不能推知“这两条直线平行”;反过来,由“两条直线平行”可知“这两条直线没有公共点”.因此,在空间中,“两条直线没有公共点”是“这两条直线平行”的必要不充分条件,选B.
6. 已知函数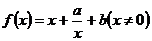 ,其中
,其中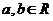 .
.
(1)若曲线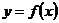 在点
在点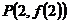 处的切线方程为
处的切线方程为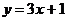 ,求函数
,求函数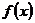 的解析式;
的解析式;
(2)讨论函数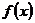 的单调性;
的单调性;
(3)若对于任意的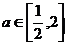 ,不等式
,不等式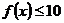 在
在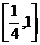 上恒成立,求
上恒成立,求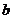 的取值范围.
的取值范围.
|
批阅时间 |
等级 |
|
|
|
5. 已知:命题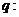 集合
集合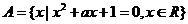 ,
, ,且
,且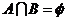
(I)若命题q为真命题,求实数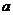 的取值范围;
的取值范围;
(II)若命题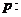
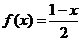 ,且
,且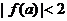 ,试求实数
,试求实数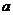 的取值范围,使得命题
的取值范围,使得命题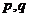 有且只有一个为真命题.
有且只有一个为真命题.
4. 对于函数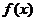 定义域中任意
定义域中任意 有如下结论:
有如下结论:
(1)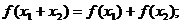 (2)
(2)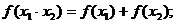 (3)
(3)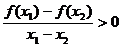 (4)
(4)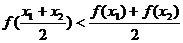 。当
。当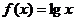 时,上述结论中正确结论的序号是
时,上述结论中正确结论的序号是 。
。
3. 已知命题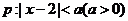 ,命题
,命题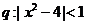 ,若
,若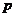 是
是 的充分不必要条件,则实数
的充分不必要条件,则实数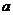 的取值范围是
.
的取值范围是
.
2. 已知 ,
,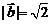 ,且
,且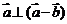 ,则向量
,则向量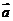 与向量
与向量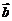 的夹角是 。
的夹角是 。
1. 命题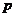 :
: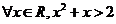 ,则命题
,则命题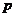 的否定为
。
的否定为
。
6. 已知函数 .
.
(1)若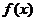 为奇函数,求a的值;(2)若
为奇函数,求a的值;(2)若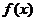 在
在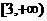 上恒大于0,求a的取值范围.
上恒大于0,求a的取值范围.
|
批阅时间 |
等级 |
|
|
|
姓名 作业时间: 年 月 日 星期 作业编号 024
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com