13．(2009·江苏，12)设α和β为不重合的两个平面，给出下列命题：

(1)若α内的两条相交直线分别平行于β内的两条直线，则α平行于β；

(2)若α外一条直线l与α内的一条直线平行，则l和α平行；

(3)设α和β相交于直线l，若α内有一条直线垂直于l，则α和β垂直；

(4)直线l与α垂直的充分必要条件是l与α内的两条直线垂直．

上面命题，真命题的序号是________(写出所有真命题的序号)

答案：(1)(2)

解析：由面面平行的判定定理可知，(1)正确．

由线面平行的判定定理可知，(2)正确．

对于(3)来说，α内直线只垂直于α和β的交线l，得不到其是β的垂线，故也得不出α⊥β.

对于(4)来说，l只有和α内的两条相交直线垂直，才能得到l⊥α.

也就是说当l垂直于α内的两条平行直线的话，l不一定垂直于α.

12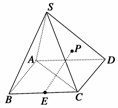．(2010·辽宁省东北育才中学高三模拟)如图在正四棱锥S－ABCD中，E是BC的中点，P点在侧面△SCD内及其边界上运动，并且总是保持PE⊥AC，则动点P的轨迹与△SCD组成的相关图形是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　 (　)

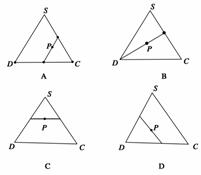
答案：D

解析：取CD中点F，AC⊥EF，又∵SD在面ABCD内的射影为BD且AC⊥BD，∴AC⊥SD，取SC中点Q，∴EQ∥SD，

∴AC⊥EQ，又AC⊥EF，∴AC⊥面EQF，因此点P在FQ上移动时总有AC⊥EP.故选D.

第Ⅱ卷(非选择题　共90分)

11．一个正三棱锥的四个顶点都在半径为1的球面上，其中底面的三个顶点在该球的一个大圆上，则该正三棱锥的体积是　　　　　　　　　　　　　　　　 (　)

A.　 　　　　　　　 B.　 　　　　　 C.　 　　　　　 D.

答案：C

解析：由题意易知正三棱锥的顶点到底面的距离为1.

∵底面是正三角形且球半径为1.

∴底面边长为，∴底面积为，

∴V＝××1＝.

10．如图所示，在单位正方体ABCD－A₁B₁D₁的面对角线A₁B上存在一点P使得AP+D₁P取得最小值，则此最小值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

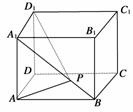
A．2　 　　　　　　　　　　　　　　　　　　　 B.

C．2+　 　　　　　　　　　　　　　　　 D.

答案：D

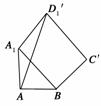解析：如图所示，把对角面A₁C绕A₁B旋转至A₁BC′D₁′，使其与△AA₁B在同一平面上，连接AD₁′，则AD₁′＝＝为所求的最小值．

9．如图，α⊥β，α∩β＝l，A∈α，B∈β，A、B到l的距离分别是a和b.AB与α、β所成的角分别是θ和φ，AB在α、β内的射影分别是m和n.若a＞b，则　　　　　　　　　　　 (　)

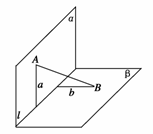A．θ＞φ，m＞n

B．θ＞φ，m＜n

C．θ＜φ，m＜n

D．θ＜φ，m＞n

答案：D

解析：由题意可得

即有故选D.

8．如图，在棱长为3的正方体ABCD－A₁B₁C₁D₁中，M、N分别是棱A₁B₁、A₁D₁的中点，则点B到平面AMN的距离是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

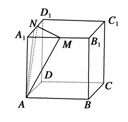A.　 　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　 D．2

答案：D

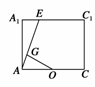
解析：设AC的中点为O，MN的中点为E，连结AE，作OG⊥AE于G，易证OG即是点B到平面AMN的距离．作出截面图，如图所示，由AA₁＝3，AO＝，AE＝，△AA₁E∽△OGA，计算得OG＝2，故选D.

7．已知三棱锥P－ABC的三个侧面与底面全等，且AB＝AC＝，BC＝2.则二面角P－BC－A的大小为　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.　 B.　 C.　 D.

答案：C

解析：如图所示，由三棱锥的三个侧面与底面全等，且AB＝AC＝，

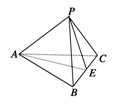得PB＝PC＝，

PA＝BC＝2，

取BC的中点E，连结AE，PE，

则∠AEP即为所求二面角的平面角．

且AE＝EP＝，

∵AP²＝AE²+PE²，∴∠AEP＝.

6．正四棱柱ABCD－A₁B₁C₁D₁中，对角线BD₁＝8，BD₁与侧面BC₁所成的角为30°，则BD₁和底面ABCD所成的角为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．30°　 B．60°　 C．45°　 D．90°

答案：C

解析：∵BD₁与侧面BC₁所成的角为∠D₁BC₁，则∠D₁BC₁＝30°.

又BD＝8，∴D₁C₁＝4，∴BD＝4.

又D₁B与底面ABCD所成的角为∠D₁BD，

从而cos∠D₁BD＝＝，

∴∠D₁BD＝45°.

5．在直三棱柱ABC－A₁B₁C₁中，AA₁＝AB＝AC，AB⊥AC，M是CC₁的中点，Q是BC的中点，点P在A₁B₁上，则直线PQ与直线AM所成的角等于　　　　　　　　　　　　　　 (　)

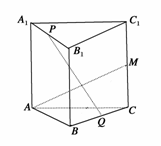A．30°　 B．45°　 C．60°　 D．90°

答案：D

解析：取AC的中点N，连结AN、QN，

可证：

⇒

　 　　⇒

　 　　　　　⇒AM⊥PQ.

故选D.

4．(2009·安徽皖北联考)已知三棱锥的三个侧面两两垂直，三条侧棱长分别为4,4,7，若此三棱锥的各个顶点都在同一球面上，则此球的表面积是　　　　　　　　　　　　　　　　　　　 (　)

A．81π　 B．36π　 C.π　 D．144π

答案：A

解析：由于三棱锥的三个侧面两两垂直，即可把它补成长方体，其对角线长为9，外接球的半径为，则球的表面积为81π，故选A.