
题目列表(包括答案和解析)
1.已知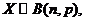 且
且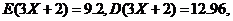 则 (
B )
则 (
B )
A.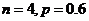 B.
B.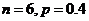 C.
C.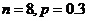 D.
D.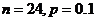
2 集合A={x|x=2k,k∈Z},B={x|x=2k+1,k∈Z},C={x|x=4k+1,k∈Z},又a∈A,b∈B,则有 ( B )
A.a+b∈A B.a+b∈B C.a+b∈C D.a+b不属于A,B,C中的任意一个
22.(2009·深圳调考一)(本小题满分12分)如图所示,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在平面和圆O所在的平面互相垂直.已知AB=2,EF=1.
(1)求证:平面DAF⊥平面CBF;
(2)求直线AB与平面CBF所成角的大小;
(3)当AD的长为何值时,二面角D-FE-B的大小为60°?
解析:(1)证明:∵平面ABCD⊥平面ABEF,CB⊥AB,
平面ABCD∩平面ABEF=AB,
∴CB⊥平面ABEF.
∵AF⊂平面ABEF,∴AF⊥CB,
又∵AB为圆O的直径,∴AF⊥BF,
 ∴AF⊥平面CBF.
∴AF⊥平面CBF.
∵AF⊂平面DAF,∴平面DAF⊥平面CBF.
(2)解:根据(1)的证明,有AF⊥平面CBF,
∴FB为AB在平面CBF上的射影,
因此,∠ABF为直线AB与平面CBF所成的角.
∵AB∥EF,∴四边形ABEF为等腰梯形,
过点F作FH⊥AB,交AB于H.
AB=2,EF=1,则AH==.
在Rt△AFB中,根据射影定理AF2=AH·AB,得AF=1,
sin∠ABF==,∴∠ABF=30°,
∴直线AB与平面CBF所成角的大小为30°.
(3)解:过点A作AM⊥EF,交EF的延长线于点M,连结DM.
根据(1)的证明,DA⊥平面ABEF,则DM⊥EF,
∴∠DMA为二面角D-FE-B的平面角,
∠DMA=60°.
在Rt△AFH中,∵AH=,AF=1,
∴FH=.
又∵四边形AMFH为矩形,∴MA=FH=.
∵AD=MA·tan∠DMA=·=.
因此,当AD的长为时,二面角D-FE-B的大小为60°.
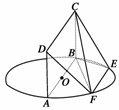
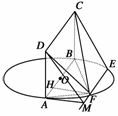
21.(2009·安徽,18)(本小题满分12分)如图所示,四棱锥F-ABCD的底面ABCD是菱形,其对角线AC=2,BD=.AE、CF都与平面ABCD垂直,AE=1,CF=2.
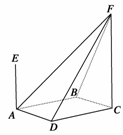
(1)求二面角B-AF-D的大小;
(2)求四棱锥E-ABCD与四棱锥F-ABCD公共部分的体积.
命题意图:本题考查空间位置关系,二面角平面角的作法以及空间几何体的体积计算等知识.考查利用综合法或向量法解决立体几何问题的能力.
解答:(1)解:连接AC、BD交于菱形的中心O,过O作OG⊥AF,G为垂足,连接BG、DG.
由BD⊥AC,BD⊥CF得BD⊥平面ACF,故BD⊥AF.
于是AF⊥平面BGD,所以BG⊥AF,DG⊥AF,∠BGD为二面角B-AF-D的平面角.
由FC⊥AC,FC=AC=2,得∠FAC=,OG=.
由OB⊥OG,OB=OD=,得∠BGD=2∠BGO=.
(2)解:连接EB、EC、ED,设直线AF与直线CE相交于点H,则四棱锥E-ABCD与四棱锥F-ABCD的公共部分为四棱锥H-ABCD.
过H作HP⊥平面ABCD,P为垂足.
因为EA⊥平面ABCD,FC⊥平面ABCD,
所以平面ACEF⊥平面ABCD,从而P∈AC,HP⊥AC.
由+=+=1,得HP=.
又因为S菱形ABCD=AC·BD=,
故四棱锥H-ABCD的体积V=S菱形ABCD·HP=.
20.(本小题满分12分)(2010·唐山市高三摸底考试)如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,N是A1D的中点,M∈BB1,异面直线MN与A1A所成的角为90°.
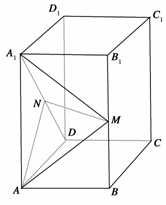
(1)求证:点M是BB1的中点;
(2)求直线MN与平面ADD1A1所成角的大小;
(3)求二面角A-MN-A1的大小.
解析:(1)取AA1的中点P,连结PM,PN.
∵N是A1D的中点,∴AA1⊥PN,又∵AA1⊥MN,MN∩PN=N,
∴AA1⊥面PMN.
∵PM⊂面PMN,∴AA1⊥PM,∴PM∥AB,
∴点M是BB1的中点.
(2)由(1)知∠PNM即为MN与平面ADD1A1所成的角.
在Rt△PMN中,易知PM=1,PN=,
∴tan∠PNM==2,∠PNM=arctan2.
故MN与平面ADD1A1所成的角为arctan2.
(3)∵N是A1D的中点,M是BB1的中点,∴A1N=AN,A1M=AM,
又MN为公共边,∴△A1MN≌△AMN.
在△AMN中,作AG⊥MN交MN于G,连结A1G,则∠A1GA即为二面角A-MN-A1的平面角.
在△A1GA中,AA1=2,A1G=GA=,
∴cos∠A1GA==-,∴∠A1GA=arccos(-),
故二面角A-MN-A1的大小为arccos(-).
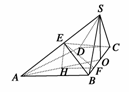
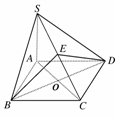
19. (本小题满分12分)如图,四棱锥S-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=SB=SC=2CD=2,侧面SBC⊥底面ABCD.
(本小题满分12分)如图,四棱锥S-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=SB=SC=2CD=2,侧面SBC⊥底面ABCD.
(1)由SA的中点E作底面的垂线EH,试确定垂足H的位置;
(2)求二面角E-BC-A的大小.
解析:(1)作SO⊥BC于O,则SO⊂平面SBC,
又面SBC⊥底面ABCD,
面SBC∩面ABCD=BC,
∴SO⊥底面ABCD①
 又SO⊂平面SAO,∴面SAO⊥底面ABCD,
又SO⊂平面SAO,∴面SAO⊥底面ABCD,
作EH⊥AO,∴EH⊥底面ABCD②
即H为垂足,由①②知,EH∥SO,
又E为SA的中点,∴H是AO的中点.
(2)过H作HF⊥BC于F,连结EF,
由(1)知EH⊥平面ABCD,∴EH⊥BC,
又EH∩HF=H,∴BC⊥平面EFH,∴BC⊥EF,
∴∠HFE为面EBC和底面ABCD所成二面角的平面角.
在等边三角形SBC中,∵SO⊥BC,
∴O为BC中点,又BC=2.
∴SO==,EH=SO=,
又HF=AB=1,
∴在Rt△EHF中,tan∠HFE===,
∴∠HFE=arctan.
即二面角E-BC-A的大小为arctan.
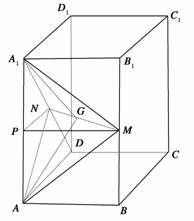
18.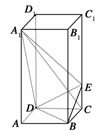 (本小题满分12分)如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在C1C上且C1E=3EC.
(本小题满分12分)如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在C1C上且C1E=3EC.
(1)证明A1C⊥平面BED;
(2)求二面角A1-DE-B的大小.
解析:依题设知AB=2,CE=1,
(1)证明:连结AC交BD于点F,则BD⊥AC.
由三垂线定理知,BD⊥A1C.
在平面A1CA内,连结EF交A1C于点G,
由于==2,
故Rt△A1AC∽Rt△FCE,∠AA1C=∠CFE,∠CFE与∠FCA1互余.
于是A1C⊥EF.
A1C与平面BED内两条相交直线BD、EF都垂直.
所以A1C⊥平面BED.
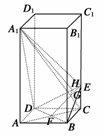 (2)作GH⊥DE,垂足为H,连结A1H.
(2)作GH⊥DE,垂足为H,连结A1H.
由三垂线定理知A1H⊥DE,
故∠A1HG是二面角A1-DE-B的平面角.
EF==,
CG== .
EG==.
=,GH=×= .
又A1C==2,A1G=A1C-CG=,
tan∠A1HG==5.
所以二面角A1-DE-B的大小为arctan5.
17.(本小题满分10分)如图,四棱锥S-ABCD的底面是正方形,SA⊥底面ABCD,E是SC上一点.
(1)求证:平面EBD⊥平面SAC;
(2)假设SA=4,AB=2,求点A到平面SBD的距离;
解析:(1)∵正方形ABCD,∴BD⊥AC,又∵SA⊥平面ABCD,∴SA⊥BD,则BD⊥平面SAC,又BD⊂平面BED,∴平面BED⊥平面SAC.
(2)设AC∩BD=O,由三垂线定理得BD⊥SO.AO=AC=AB=··2=,SA=4,则SO===3,S△BSD=BD·SO=·2·3=6.设A到面BSD的距离为h,则VS-ABD=VA-BSD,即S△ABD·SA=S△BSD·h,解得h=,即点A到平面SBD的距离为.
16.如图,已知球O的面上四点A、B、C、D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=,则球O的体积等于________.
答案:π
解析:△ABC的外接圆的直径为AC,AC=,由DA⊥面ABC得DA⊥AC,
∴CD为球的直径,CD==3,
∴球的半径R=,
∴V球=πR3=π.
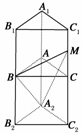
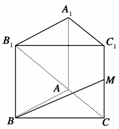
15.(2009·四川,15)如图所示,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是________.
答案:90°
解析:设棱长为a,补正三棱柱ABC-A2B2C2(如图).平移AB1至A2B,连结A2M,∠MBA2即为AB1与BM所成的角,在△A2BM中,A2B=a,
BM==a,
A2M==a,
∴A2B2+BM2=A2M2,∴∠MBA2=90°.
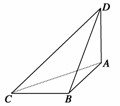
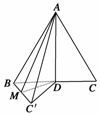
14.如图所示,等边△ABC的边长为4,D为BC中点,沿AD把△ADC折叠到△ADC′处,使二面角B-AD-C′为60°,则折叠后点A到直线BC′的距离为________;二面角A-BC′-D的正切值为________.
 答案: 2
答案: 2
解析:如图,作DM⊥BC′于点M,连结AM,则AM为点A到直线BC′的距离,AD=2,DM=,所以AM==.二面角A-BC′-D的平面角为∠AMD,正切值为tan∠AMD==2.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com