8．△ABC中，已知b＝10，c＝15，C＝30°，则此三角形的解的情况是　　　　　 (　)

A．一解　 　　　　　　　　　 B．两解　 　　　　　　　　　 C．无解　 　　　　　　　　　 D．无法确定

答案：A

解析：由b＜c得B＜C，B必为小于30°的锐角．

7．设平面上有四个互异的点A、B、C、D，已知(+－2)·(－)＝0，则△ABC的形状是　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．直角三角形　 　　　　　　　　　　　 B．等腰三角形

C．等腰直角三角形　 　　　　　　　 D．等边三角形

答案：B

解析：(+－2)·(－)＝0

即(+)·(－)＝0

∴AB²－AC²＝0，即||＝||.

6．函数f(x)＝2sin(x+θ)的图象按向量a＝(，0)平移后，它的一条对称轴为x＝，则θ的一个可能值是　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.　 　　　　　　　　　　　　 B.　 　　　　　　　　　　　　 C.　 　　　　　　　　　　　　　 D.

答案：B

解析：设P(x，y)是f(x)＝2sin(x+θ)的图象上任一点按向量a＝(，0)平移后的点P′(x′，y′)．则　∴

∴y′＝2sin(x′+θ－)

而它的一条对称轴为x＝.

∴+θ－＝kπ+，k∈Z

∴θ＝kπ++.k∈Z.

当k＝0时，θ＝.故选B.

5．设点P分有向线段的比为，则点P₁分所成的比为　　　　　　　　　　　　 (　)

A．－　 　　　　　　　　　　 B．－ 　　　　　　　　　　　 C.　 　　　　　　　　　　　　　 D.

答案：A

解析：由条件知P内分，∴P₁外分易求得A.

4．(2009·北京市海淀区高三年级第一学期期末练习)已知向量a＝(1,0)与向量b＝(－1，)，则向量a与b的夹角为　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.　 　　　　　　　　　　　　　 B.　 　　　　　　　　　　　　　 C.　 　　　　　　　　　　　　 D.

答案：C

解析：设向量a、b的夹角等于θ，依题意得，a·b＝|a||b|cosθ，－1＝1×2cosθ，cosθ＝－，又θ∈[0，π]，因此θ＝，选C.

3．已知向量a＝(1,2)，b＝(x+1，－x)，且a⊥b，则x＝　　　　　　　　　　　　　　　　 (　)

A．1　　　　　　　　 B．2　　　　　　　　　 C.　　　　　　　　　　 D．0

答案：A

解析：∵a⊥b，∴a·b＝0，即x+1－2x＝0，x＝1.故选A.

2．(2009·福建厦门)如图所示，已知＝a，＝b，＝3，用a、b表示，则＝

(　)

A．a+b　 　　　　　　　　　　　　　　　 B.a+b

C.a+b　 　　　　　　　　　　　　　　　　 D.a+b

答案：B

解析：＝－＝b－a.

＝+＝+＝a+(b－a)＝a+b，故选B.

1．向量a与b(b≠0)共线的充要条件是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．a＝b　　　　　　　　　　　　 B．a－b＝0

C．a²－b²＝0　 　　　　　　　　　　　　 D．a+λb＝0(λ∈R)

答案：D

11.已知: 直线, 且直线与a, b, c都相交．

求证: 直线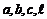共面．

10.正方体ABCD-A₁B₁C₁D₁中，E，F分别是AB和AA₁的中点，

求证：(1)E、C、D₁、F四点共面；(2)CE、D₁F、DA三线共点