
题目列表(包括答案和解析)
8.(2010·马鞍山质检)给出下列结论:


 ①命题“若p,则q或r”的否命题是“若 p,则 q且 r”;
①命题“若p,则q或r”的否命题是“若 p,则 q且 r”;

 ②命题“若 p,则q”的逆否命题是“若p,则 q”;
②命题“若 p,则q”的逆否命题是“若p,则 q”;
③命题“∃n∈N*,n2+3n能被10整除”的否命题是“∀n∈N*,n2+3n不能被10整除”;
④命题“∀x,x2-2x+3>0”的否命题是“∃x,x2-2x+3<0”.
其中正确结论的个数是 ( )
A.1 B.2 C.3 D.4
解析:由于否命题是把原命题的否定了的条件作条件、否定了的结论作结论得到的命题,故①正确;由于逆否命题是把原命题的否命题了的结论作条件、否定了的条件作结论得到的命题,故②不正确;特称命题的否命题是全称命题,故③正确;虽然全称命题的否命题是特称命题,但对结论的否定错误,故④不正确.
答案:B
第Ⅱ卷 (非选择题,共110分)
7.已知a,b为实数,则2a>2b是log2a>log2b的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
解析:p:2a>2b⇔a>b;q:log2a>log2b⇔a>b>0,
故p q,q⇒p,∴p是q的必要不充分条件.
q,q⇒p,∴p是q的必要不充分条件.
答案:B
6.(2010·海口模拟)已知集合A={x∈R|<2x<8},B={x∈R|-1<x<m+1},若x∈B成立的一个充分不必要的条件是x∈A,则实数m的取值范围是 ( )
A.m≥2 B.m≤2 C.m>2 D.-2<m<2
解析:A={x∈R|<2x<8}={x|-1<x<3},
∵x∈B成立的一个充分不必要条件是x∈A,
∴A B,
B,
∴m+1>3,即m>2.
答案:C
5.下列特称命题中,假命题是 ( )
A.∃x∈R,x2-2x-3=0 B.至少有一个x∈Z,x能被2和3整除
C.存在两个相交平面垂直于同一直线 D.∃x∈{x|x是无理数},使x2是有理数
解析:对于A:当x=-1时,x2-2x-3=0,故A为真命题;
对于B:当x=6时,符合题目要求,为真命题;
对于C假命题;
对于D:x=时,x2=3,故D为真命题.
综上可知:应选C.
答案:C
4.已知a,b是实数,则“a>0且b>0”是“a+b>0且ab>0”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
解析:当a>0且b>0时,一定有a+b>0且ab>0.反之,当a+b>0且ab>0时,一定有a>0,b>0.故“a>0且b>0”是“a+b>0且ab>0”的充要条件.
答案:C
3.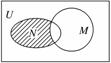 (2010·东北师大附中模拟)设全集U是实数集R,M={x|x2>
(2010·东北师大附中模拟)设全集U是实数集R,M={x|x2>
4},N={x|x≥3或x<1}都是U的子集,则图中阴影部分所
表示的集合是 ( )
A.{x|-2≤x<1} B.{x|-2≤x≤2}
C.{x|1<x≤2} D.{x|x<2}
解析:图中阴影部分表示N∩(∁UM),∵M={|x2>4}={x|x>2或x<-2},
∴∁UM={x|-2≤x≤2},∴N∩(∁UM)={-2≤x<1}.
答案:A
2.集合P={m2|m∈N*},若a,b∈P,则a⊗b∈P,那么运算⊗可能是 ( )
A.加法 B.减法 C.乘法 D.除法
解析:特例:a=1,b=4.
答案:C
1.已知集合A={1,3,5,7,9},B={0,3,6,9,12},则A∩(∁NB)= ( )
A.{1,5,7} B.{3,5,7} C.{1,3,9} D.{1,2,3}
解析:∵A={1,3,5,7,9},B={0,3,6,9,12},∴∁NB={1,2,4,5,7,8,……}.
∴A∩(∁NB)={1,5,7}.
答案:A
例3 解方程: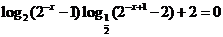 。
。
分析:形如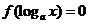 的对数方程,可采用换元法进行求解。
的对数方程,可采用换元法进行求解。
解析:原方程可化为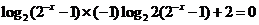 ,
,
即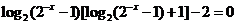 。
。
令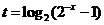 ,则
,则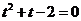 ,解之得
,解之得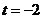 或
或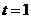 ,
,
∴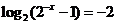 ,或
,或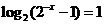 。
。
解得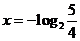 或
或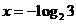 。
。
检验可知,以上两根都是原方程的根。
评注:在解对数方程时,要注意将根代入原方程检验,将不满足原方程的根去掉。
例4 设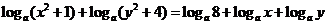 ,求实数
,求实数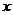 、
、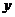 的值。
的值。
分析:在一个方程中含有两个未知数,必须运用特殊方法进行求解,本题可用非负数的性质求解。
解析:由题意可得,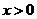 ,
,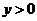 ,
,
原方程可化为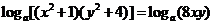 ,
,
即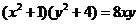 。
。
∴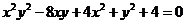 ,∴
,∴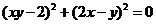 。
。
∴由非负数的性质得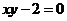 ,且
,且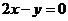 ,∴
,∴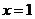 ,
,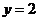 。
。
评注:通过拆项配方,使问题巧妙获解。
例1 解方程: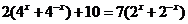 。
。
分析:该例可采用换元法求解。
解析:令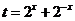 ,则
,则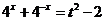 ,
,
∴原方程变形为 ,解得
,解得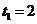 ,
,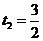 。
。
由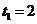 得
得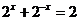 ,∴
,∴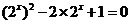 ,
,
即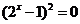 ,∴
,∴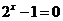 ,∴
,∴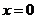 。
。
由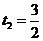 得
得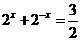 ,∴
,∴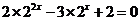 ,
,
∵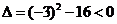 ,∴此方程无实根。
,∴此方程无实根。
故原方程的解为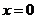 。
。
评注:将指数方程转化为基本型求解,是解决该类问题的关键。
例2 解方程: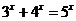 。
。
分析:利用指数函数的单调性进行求解。
解析:原方程等价于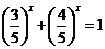 ,显然
,显然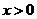 。
。
构造函数
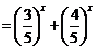 ,则
,则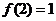 ,即
,即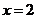 是原方程的根。
是原方程的根。
∵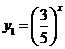 ,
,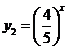 都是减函数,∴
都是减函数,∴ 也是减函数,
也是减函数,
当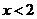 时,
时,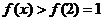 ;当
;当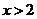 时,
时,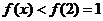 。
。
故原方程只有一个解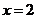 。
。
评注:灵活运用指数函数的性质,提高解题能力。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com