
题目列表(包括答案和解析)
2.等差数列{an}的通项公式是an=1-2n,其前n项和为Sn,则数列{}的前11项和为
( )
A.-45 B.-50 C.-55 D.-66
解析:Sn=,∴==-n,
∴{}的前11项的和为-66.
答案:D
1.已知实数列-1,x,y,z,-2成等比数列,则xyz等于 ( )
A.-4 B.±4 C.-2 D.±2
解析:∵xz=(-1)×(-2)=2,y2=2,∴y=-(正不合题意),∴xyz=-2.
答案:C
例3 在平面几何中,经过直线外一点有且只有一条直线和这条直线平行,这个结论在
空间中是否成立?
解:在空间中这个结论也成立.下面用反证法证明:
假设结论在空间中不成立,那么过直线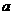 外一点
外一点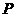 有两条直线
有两条直线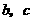 与
与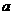 平行,
平行,
即有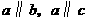 .由平行公理知,
.由平行公理知,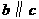 ,这与
,这与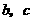 有公共点矛盾.
有公共点矛盾.
所以,该结论在空间仍然成立.
点评:一般情况下,要把平面几何中的结论推广到立体几何中,需要经过证明才能使用,千万不能盲目套用.
例2
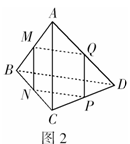 如图2,在空间四边形
如图2,在空间四边形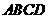 中,
中, 分
分
别是四边形边上的点,且满足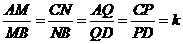 .
.
求证: 四点共面且四边形
四点共面且四边形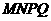 为平行四边形.
为平行四边形.
证明: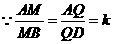 ,
,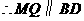 ,
,
且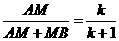 .
.
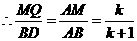 ,即
,即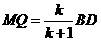 .
.
又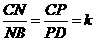 ,
,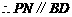 ,且
,且 .
.
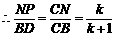 ,即
,即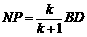 .
.
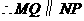 ,且
,且 .
.

 共面且四边形
共面且四边形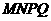 为平行四边形.
为平行四边形.
点评:要证明 四点共面,只需证明直线
四点共面,只需证明直线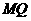 与直线
与直线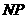 平行即可,这也是平行四边形
平行即可,这也是平行四边形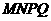 所必需的,因此,问题就转化为利用直线的传递性,寻找第三条直线分别与所求两条直线平行.
所必需的,因此,问题就转化为利用直线的传递性,寻找第三条直线分别与所求两条直线平行.
例1
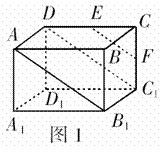 如图1,在长方体
如图1,在长方体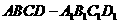 中,
中,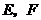 分
分
别是 的中点,求证:
的中点,求证: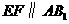 .
.
证明:连结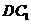 ,在长方体
,在长方体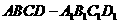 中,有
中,有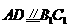 .
.
 四边形
四边形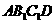 是平行四边形,
是平行四边形,
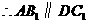 .
.
在 中,
中,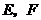 分别是
分别是 的中点,
的中点,
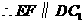 .
.
由公理4知,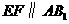 .
.
点评:判断两条直线平行的基本方法是分别寻找与这两条直线平行的第三条直线,再利用平行线的传递性就能证得这两条直线平行.
2.画法:斜二测画法.
1.定义:用来表示空间图形的平面图形,叫做空间图形的直观图.
4.组合体的三视图
应先分析组合体的组合形式,把组合体分解成基本的几何体,再按基本几何体画图,就可以画出组合体的三视图.
3.柱、锥、台、球的三视图
(1)圆柱的正视图和侧视图都是矩形,俯视图是一个圆.
(2)圆锥的正视图和侧视图都是三角形,俯视图是圆和圆心.
(3)圆台的正视图和侧视图都是等腰梯形,俯视图是两个同心圆.
(4)球的三视图都是圆.
2.三视图的排列规则
一个物体的三视图的排列规则是:俯视图放在正视图的下面,长度与正视图的长度一样;侧视图放在正视图的右面,高度与正视图的高度一样,宽度与俯视图的宽度一样.为了便于记忆,通常说:“长对正,高平齐,宽相等”或者说“正侧一样高,正俯一样长,俯侧一样宽”.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com