12.已知数列{a_n}满足＝(n∈N^*)，且a₁＝1，则a_n＝　　.

解析：由已知得＝，

＝，

…

＝，

a₁＝1，

左右两边分别相乘得

a_n＝1·····…···

＝

答案：

11.设等比数列{a_n}的前n项和为S_n，若a₁＝1，S₆＝4S₃，则a₄＝　　.

解析：设等比数列的公比为q，则由S₆＝4S₃知q≠1.

∴S₆＝＝.∴q³＝3.∴a₁q³＝3.

答案：3

10．各项都是正数的等比数列{a_n}中，a₂，a₃，a₁成等差数列，则的值为________．

解析：设{a_n}的公比为q(q＞0)，由a₃＝a₂+a₁，得q²－q－1＝0，

解得q＝.

从而＝q＝.

答案：

9．在等差数列{a_n}中，若a₂+a₄+a₆+a₈+a₁₀＝80，则a₇－·a₈的值为________．

解析：由已知得：(a₂+a₁₀)+(a₄+a₈)+a₆＝5a₆＝80⇒a₆＝16，又分别设等差数列首项为a₁，公差为d，

则a₇－a₈＝a₁+6d－(a₁+7d)

＝(a₁+5d)＝a₆＝8.

答案：8

8.已知等比数列{a_n}的各项均为不等于1的正数，数列{b_n}满足b_n＝lga_n，b₃＝18，b₆＝12，则数列{b_n}前n项和的最大值等于　　　　　　　 　　　　　　　　　　(　)

A.126　　　　　 　B.130　　　　　　 C.132　 　　　　　　D.134

解析：由题意可知，lga₃＝b₃，lga₆＝b₆.

又∵b₃＝18，b₆＝12，则a₁q²＝10¹⁸，a₁q⁵＝10¹²，

∴q³＝10.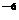

即q＝10，∴a₁＝10²².

又∵{a_n}为正项等比数列，

∴{b_n}为等差数列，且d＝－2，b₁＝22.

故b_n＝22+(n－1)×(－2)＝－2n+24.

∴S_n＝22n+×(－2)

＝－n²+23n＝－(n－)²+.

又∵n∈N^*，故n＝11或12时，

(S_n)_max＝132.

答案：C

第Ⅱ卷　(非选择题，共110分)

7．在函数y＝f(x)的图象上有点列{x_n，y_n}，若数列{x_n}是等差数列，数列{y_n}是等比数列，则函数y＝f(x)的解析式可能为　　　　　　　　　　　　　　　　　　　　　 (　)

A．f(x)＝2x+1 　　　　　　　　　B．f(x)＝4x²

C．f(x)＝log₃x　 　　　　　　　　　D．f(x)＝()^x

选D　结合选项，对于函数f(x)＝()^x上的点列{x_n，y_n}，有y_n＝()x_n.由于{x_n}是等差数列，所以x_n+1－x_n＝d，因此＝＝()x_n+1－x_n＝()^d，这是一个与n无关的常数，故{y_n}是等比数列．

6.在数列{a_n}中，a₁＝1，a₂＝2，a_n+2－a_n＝1+(－1)ⁿ，那么S₁₀₀的值等于　　　 (　)

A.2500　 　　　B.2600　　　　　 C.2700　 　　　　　　D.2800

解析：据已知当n为奇数时，

a_n+2－a_n＝0⇒a_n＝1，

当n为偶数时，a_n+2－a_n＝2⇒a_n＝n，

＝50+50×＝2600.

答案：B

5.在古希腊，毕达哥拉斯学派把1,3,6,10,15,21,28，…这些数叫做三角形数，这是因为这些数目的点可以排成一个正三角形(如图).

试问三角形数的一般表达式为　　　　　　　　　　　　　　　　　　　　　 (　)

A.n 　　　　B.n(n+1)　　　　　 C.n²－1　 　　　　　　　　D.n(n－1)

解析：由1+2+3+…+n

＝n(n+1)可得.

答案：B

4.记数列{a_n}的前n项和为S_n，且S_n＝2n(n－1)，则该数列是　　　　　　　　　 (　)

A.公比为2的等比数列　　　　　　　 B.公比为的等比数列

C.公差为2的等差数列　　　　　　　 D.公差为4的等差数列

解析：由条件可得n≥2时，a_n＝S_n－S_n－1＝2n(n－1)－2(n－1)(n－2)＝4(n－1)，当n＝1时，a₁＝S₁＝0，代入适合，故a_n＝4(n－1)，故数列{a_n}表示公差为4的等差数列.

答案：D

3.已知{a_n}是等差数列，a₄＝15，S₅＝55，则过点P(3，a₃)，Q(4，a₄)的直线斜率为(　)

A.4 　　　　　B.　　　　　　 C.－4　　　　　　　 　D.－

解析：∵{a_n}是等差数列，

∴S₅＝5a₃＝55，∴a₃＝11.

∴a₄－a₃＝15－11＝4，

∴k_PQ＝＝＝4.

答案：A